EMAT 6680 Assignment 1

Robyn Bryant and Kaycie Maddox

Problem 5: Examine graphs of y = a sin (bx+c) for different values of a, b, and c.

Since my background with trig functions is weak, I chose this problem and began with a=1, b=1, and c=0 to simply see the original sin function. I know the "shape" that a sin function has. I just needed to see its amplitude, its frequency and where it crossed the x axis.

y = sin x (red)

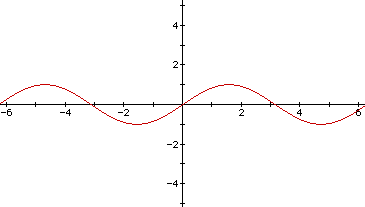
Then I tried changing 1 variable at a time to see what each variable controlled; a=2, b=1, c=0. The variable "a" controls the amplitude of the sin.

 

y = 2 sin x (green)

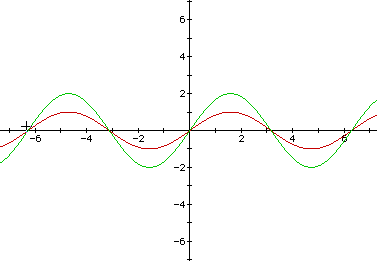
The following graph shows the variables a=1, b=1, c=2. The variable "c" moves the graph to the left or the right.

y = sin (x+2) (blue)

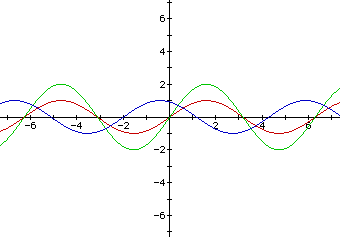
Now I want to see if I can move the graph up or down, so I am going to "guess" what will change it. None of the given variables will move it up or down, so I must need a new variable. Let's use "d". y = a sin (bx + c) + d.

y = sin x + 2 (brown)

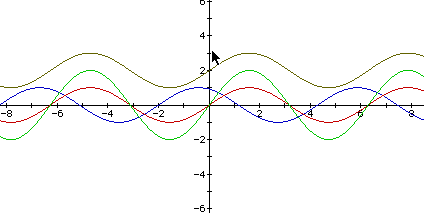
I was correct! Now I want to see if I can turn the graph around to go along the y axis. I know I must need a negative somewhere in the formula. I'm going to try a (-a) first.

y = (-1)(sin x) (purple)

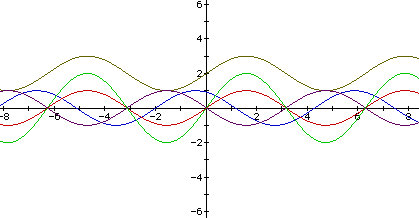
The lines are becoming a little difficult to pay attention to, but this graph was the purple one. The negative in front of the sin creates the symmetric graph to the positive sin (red one).

I will try placing the negative in another location. This time I will use it as "b". I noticed when I tried this one, that I had not tried any thing for "b" other than "1", so I made b=2. I also wanted to clear up the picture. I got the following graph:

y = sin x (green)

y = sin (2x) (red)

y = sin (-2x) (aqua)

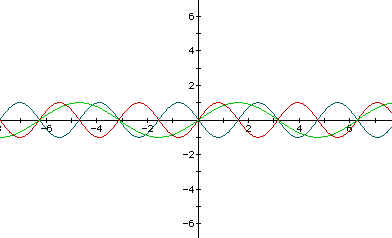
Obviously this did not turn it around the y axis either. I just discovered that the "b" controls the frequency of the sin function.

y = sin x (red)

y = sin (2x) (green)

y = sin (-2x) (blue)

y = sin (4x) (brown)

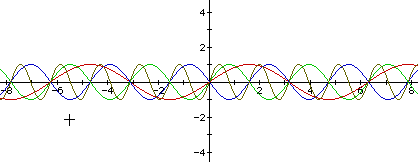
In the above graph the function y = sin (4x) has a frequency of 4 and the function y = sin (2x) has a frequency of 2. The function y = sin (-2x) also has a frequency of 2. Isn't this neat, you get to watch me learn. I just realized that the negative on the outside of the sin and the negative on the inside of the parenthesis, have the same result. For example:

y = sin x (red)

y = sin (-2x) and y = (-1)(sin (-2x)) ( green)

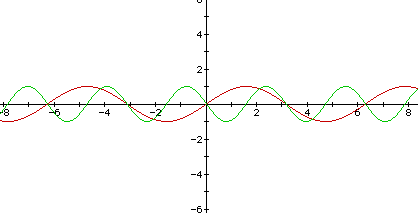
The above graph proved my hypothesis.

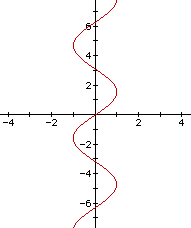
I have jumped from my earlier goal of trying to turn the sin function along the y axis. I will try it again. I've tried the negative number as "a" and "b" and neither did the job. I don't think "c" will. As a matter of fact, I know it won't because the "c" moves the graph to the left and the right.

I just had activity in my brain. I think I figured it out and I can't believe that it took this long. I don't even need a negative.

x = sin y

This was a very interesting activity for me because I needed to refresh my memory. I learned a lot more than I expected to.

 

Return