

Let's investigate what happens to two circles after we have constructed another circle tangent to the both of them. We will refer to this as the tangent circle. It becomes obvious that the tangent circle can either be internally tangent to the given circles or externally tangent to them. Here is an example of a tangent circle internally tangent to the two given circle:
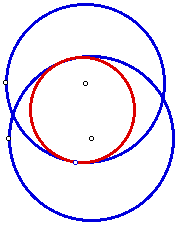
To use a script to create your own internally tangent circle, click here.
Look now at a picture of a tangent circle externally tangent to the given circles:
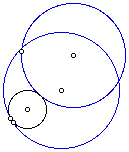
To use a script to create your own externally tangent circle, click here.
The internally tangent circle will always be on the inside of the circle with the designated point while the externally tangent circle will always be on the outside of the circle with the designated point.
We are most interested in the locus of the centers of the tangent circles. In order to investigate this, we have looked at all the possibilities. Let's begin with externally tangent circles.
Externally Tangent Circles
We will look at the case where the two given circles intersect each other:
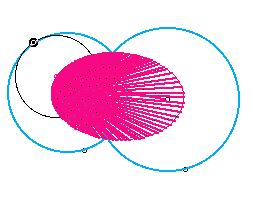
We traced the center of the tangent circle as well as the segment drawn from that center to either of the centers of the given circles. It's obvious that the locus of the segments is an ellipse. Now let's see what happens when the two given circles are tangent to one another:
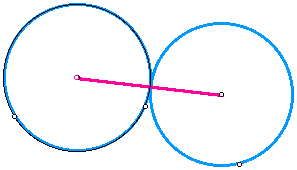
Even though it may appear that we have not found the locus of the segments, in reality there is no locus. The segment which we were tracing does not exist since the tangent and the circle on the left have the same center. If the two circles are disjoint, we will see a different locus still:
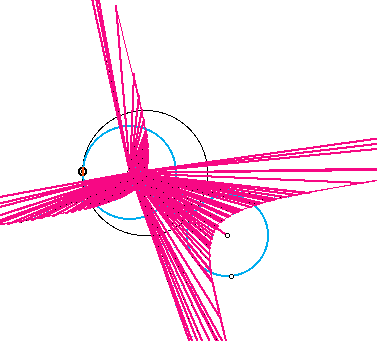
We find the locus of these segments of the circle to be a hyperbola, a sort of inside-out version of an ellipse.
Internally Tangent Circles
Now let's investigate what happens when the circle tangent to both given circles is internally tangent to them. We assume that the same results will occur. First of all, let's see what happens when the two circles intersect each other:
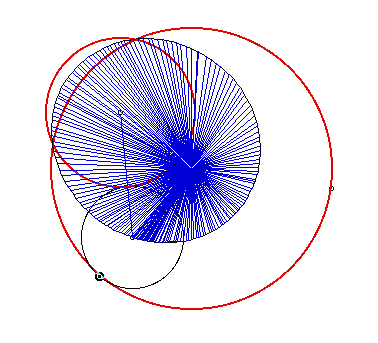
We can clearly see another ellipse with foci at the centers of the given circles. Now let's see about the case where the circles are tangent to one another:

Once again, there is no locus of points since the tangent circle is now the same circle as the circle on the right. The segment we have been tracing, therefore, does not exist since it is the one drawn between the centers of the circle on the right and the tangent circle. Finally, let's see what happens when the given circles are disjoint:
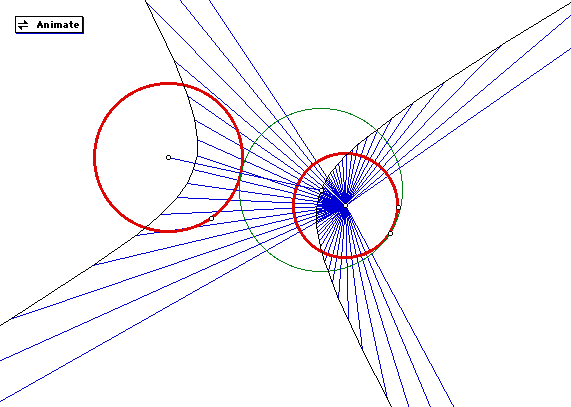
At first the blue tracing lines can be deceiving. We find that the locus of segments is the hyperbola defined by the black lines. We will leave further investigation of these events to our students. Click here to do your own investigations.