

We decided to investigate each part of this assignment and to comment on our investigations and then we will choose another to discuss further if necessary.
We constructed a script for the general construction of a pedal triangle to triangle ABC where P (the pedal point) is any point in the plane of ABC.
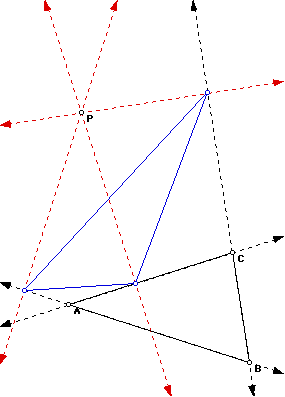
The blue triangle above is the pedal triangle of triangle ABC with point P as the pedal point. If you would like to investigate this triangle further, click here. If you would like to see or use the script to produce this triangle, click here.
The next several things we did was to create the pedal triangle of ABC when the pedal point P was in specific places. We will show you one example of each situation, but if you would like to investigate a certain situation further, you may click on the word "investigate". Here we go.
If the pedal point is the centroid of triangle ABC then you have the following situation. Investigate.
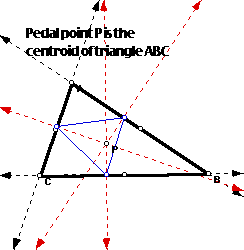
If the pedal point is the incenter of triangle ABC then you have the following situation. Investigate.
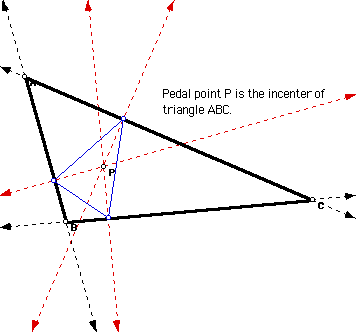
Obviously, with P being the incenter of triangle ABC, it is never located outside of triangle ABC. As a result, the pedal triangle will always remain completely inside of triangle ABC.
If P is the Circumcenter of triangle ABC then you will have the following situation. Investigate.
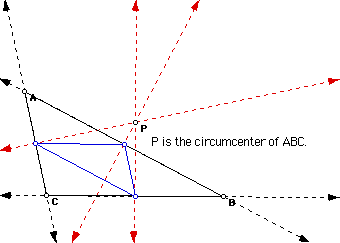
This was interesting. Although point P can go outside the triangle ABC, the pedal triangle will always remain completely inside triangle ABC.
If P is the orthocenter of triangle ABC then you have the following situation. Investigate.
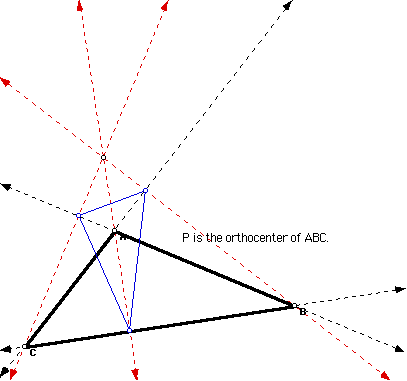
If triangle ABC becomes a right triangle, the pedal triangle becomes degenerate becoming the altitude of triangle ABC from the right angle. The orthocenter P is also becomes the right angle.
Now, speaking of degenerate triangles. A triangle is degenerate when the three vertices are collinear. This degenerate line is called the Simson Line. Click here to see for yourself when the pedal triangle becomes degenerate. We have included a "green" hint for you on that construction.
Hopefully after your investigation, you discovered that the pedal triangle is degenerate when the pedal point P lies on the circumcircle of triangle ABC. Click here to see this more clearly.
The last thing we investigated was the locus of the midpoints of the pedal triangle, when point P is animated around a circle with its center being the circumcenter of triangle ABC. To see this animation, click here.
After looking at this animation, we discovered that the 3 paths are all elipses. The elipses are all congruent when triangle ABC is an equilateral triangle. When triangle ABC is a right triangle, one of the elipses is a circle. When triangle ABC is an isosceles triangle, two of the elipses appear to be congruent to one another.
Robyn speaking here. This year is the first time I have ever heard of pedal triangles. I studied them earlier in the semester is my geometry class and again in here. I find them very interesting.
We enjoyed this activity and consider it a great one for students to work on and make conjectures and then have them try to prove their conjectures. The grade level of students would determine what method of "proof" one should accept.