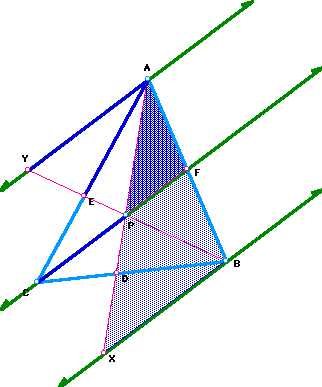
I constructed a triangle ABC and selected a point P inside the triangle. I then constructed lines AP,BP, and CP extended to their intersections with the opposite sides in points D,E, and F respectively. Below is a picture of what I began with.
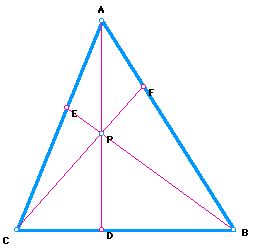
Below are a list of calculations that I did as I investigated the given segments of the construction.
Click here to investigate this calculations for yourself. You will notice that the ratio of the specific segment products will always be 1. This is my conjecture, now I will proceed to try to prove it true.
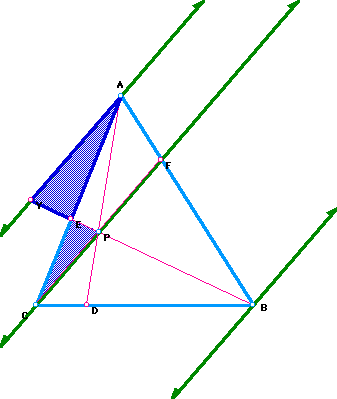
I began trying to prove my conjecture by constructing a parallel line AY to CF. I also constructed the other green line through B parallel to CF for further use. The first thing I want to do is to prove that triangle AYE is similar to triangle CPE. I can do this by showing 2 pairs of corresponding angles congruent. Angle AEY is congruent to angle CEP by vertical angles and then angle YAE is congruent to angle PCE by alternate interior angles of parallel lines.
As a result we have the following proportion
The next step includes the following picture with a few additions.
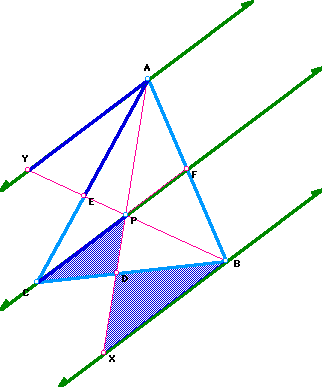
This time I am going to prove that triangle PDC is similar to triangle XDB. These triangles are similar by the same reasons the other two triangles were proven to be similar. I then get the following proportion.
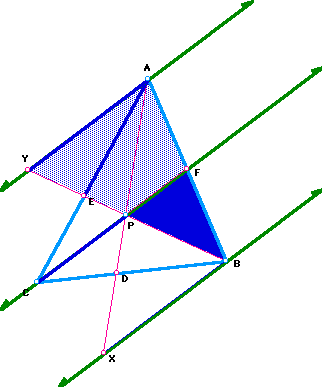
I now want to show that triangle YAB is similar to triangle PFB. Obviously angle FBP is congruent to angle ABY because it is the same angle. Then by corresponding angles, angle FPB is congruent to angle AYB. Therefore the two triangles are similar.
Triangle AFP is similar to triangle ABX and this can be proven by the same steps as in the above problem.
Let's look again at the four proportions that I now have.
Now according to the hint given to us, I must come up with this formula in my proof.
After using the other hint of parallel lines, this proof was fairly simple. I thought in advance what I would try to do with the ratios, so I knew which ratios of sides I wanted to use in my proof.
By comparing the proportions listed above, I noticed that 
included part
of the ratios listed in the proportion I wanted to prove. I simply flipped
the whole thing over and began with that.
Since a proportion is 2 equal ratios, I can multiply one side of the
above proportion with one ratio and the other side with the other ratio.
Let's begin with 
.
Let me show you what I mean.
Now that you see what I mean, I am going to apply the other two proportions. Keep in mind that if I flip one side, I did remember to flip the other side also.
Look closely at the right hand side of this equation. Do you see anything interesting? I did. Everything cancels out and I'm left with 1 on that side. On the left hand side, BA and AB cancel out. Then I'm left with
Therefore I know that the ratios of the product of the stated segments will always give us one.
You asked if this can be generalized so that point P can be outside the triangle. I will supply a picture and say "Yes".
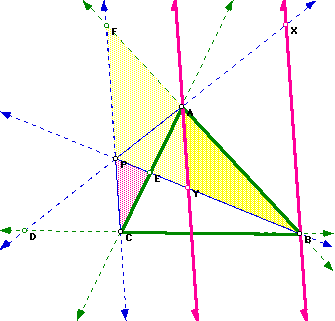
You can prove it just the same as with P on the inside of the triangle. The triangles become confusing when too many are highlighted, so I just showed 2 pairs of similar triangles here. Triangle AYE is similar to triangle CPE. Also, triangle FPB is similar to triangle AYB. If you would like to further investigate this picture, click here.
Now I am to show that when P is inside triangle ABC, the ratio of the areas of ABC and DEF is always greater than or equal to 4. I am going to show you several examples and then let you investigate it yourself.
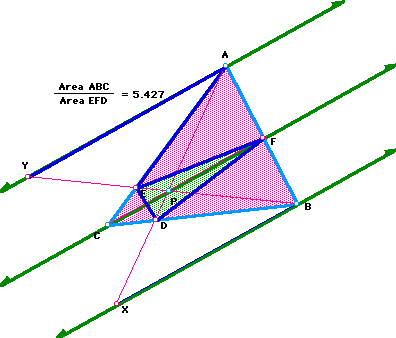
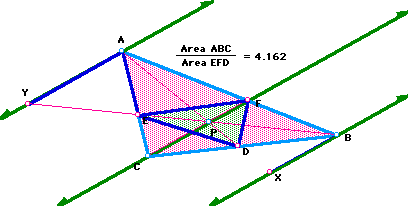
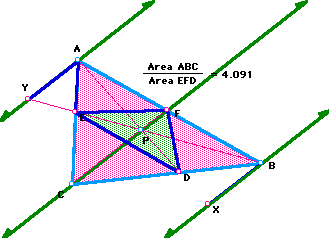
If you will notice, the closer P gets to the "center" of the triangle, the closer the ratio gets to 4.
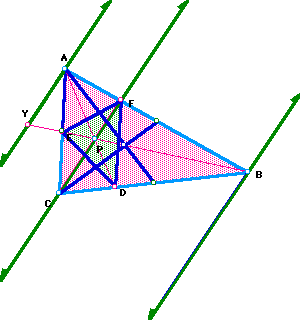
If you will notice, I constructed the centroid of triangle ABC. It is the point of intersection of the two medians. Now I am going to move P to the centroid (as close as I can get it). I predict that the ratio will be 4.
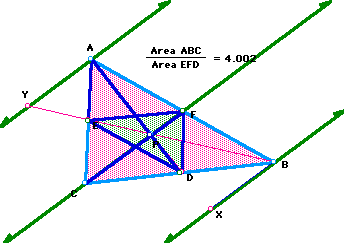
I was correct. The ratio is 4 when point P is the centroid. The end.
Thank you for a wonderful semester!