

Triangles encompass a large part of the curriculum in high school Geometry. Many high schoolers are familiar with basic concepts and properties of triangles from middle school math. This article takes an aspect of the area of triangles and gives a diverse, more indepth investigation of triangle area, namely half the area.
We begin with the Geometer's Sketchpad approach to constructing half the area of a triangle. Two cases will be discussed. The first of which is a summarization of information taken from Dr. J. Wilson's website at The University of Georgia. The second will look at my own discovery of finding half the area of a triangle.
Next we move to a discussion of whether the segments, which bisects the area for each base, are concurrent.
Finally, we will discuss if there is any relevance or significance to the triangle formed by the intersection of the three segments for each base in half a triangle.
CONSTRUCTION OF HALF A TRIANGLE: Case 1
The following figures are a layout of how one can construct half the area of a triangle. Using any triangle, say ABC, one can construct a parallel segment to a base such that it divides the area of the two parts equally. The construction can be made by hand, but is more reasonable using Geometer's Sketchpad.
Begin with any triangle, say ABC, and using one side of the triangle, make a circle by center (C) and radius (CB). Now construct a perpendicular line to the radius (CB) through the center (C) and place a point of intersection (B').
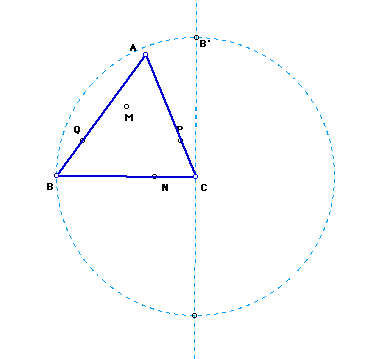
Next, construct segment BB' (shown below).
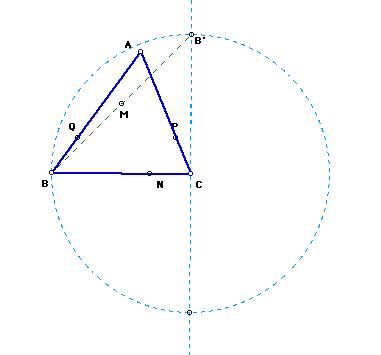
Continue by selecting the midpoint of BB' and making a circle by center (B) and radius (BM).
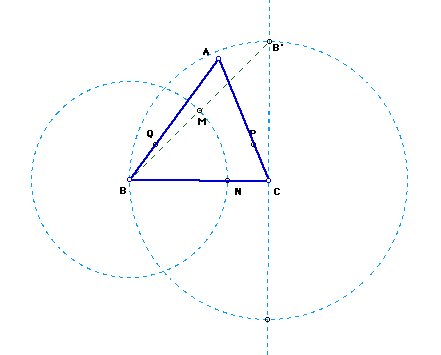
Now, construct a point of intersection (N) between the triangle and the new circle . Construct a parallel line to the opposite side (AB) that runs through the latest point of intersection (N). A point of intersection with the other side of the triangle (P) is placed next.
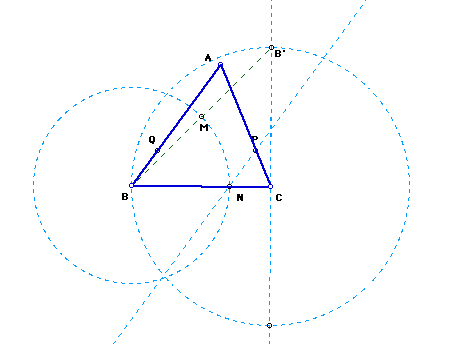
A segment or line through the new point (P) and parallel to the base (BC) is constructed in order to divide the triangle into two congruent areas.
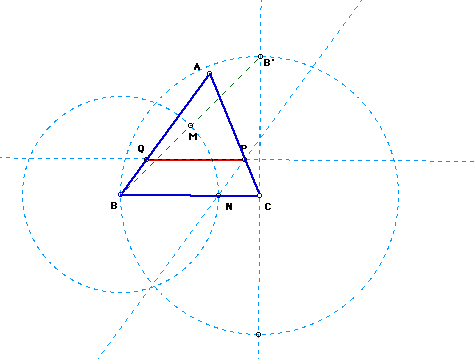
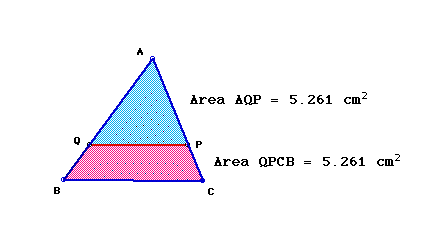
The graphic below shows the equal areas. Click here to investigate the figure below own your own and see that the areas maintain equality.
CONSTRUCTION OF HALF A TRIANGLE: Case 2
Further investigation of the above led me to begin wandering what relationship the altitude has to half the area of a triangle. Since triangleAQP is similar to triangle ABC by AA, I decided to set up a ratio of the altitudes (height) of the smaller triangle (AE) to the larger triangle(AD). The ratio yields .707 and maintains this ratio when manipulated. A picture is shown below for the set up of the said triangle.
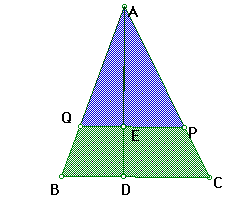
To view click here.
Furthermore, I began to investigate the relationship of the area of the triangle, AQP, to the area of the trapezoid, QPCB. Taking into account that when we have "half a triangle", the area of triangle AQP is equal to the area of trapezoid QPCB, we used the information gained from sketchpad manipulations to set up the chart below. The layout of the equation shows the ratio of the sides of the triangle in a written form. Therefore, when bisecting the area of a triangle using a parallel segment to a base, the ratio of the sides is .707.
CONCURRENT SEGMENTS?
Now the question has arisen as to whether the sement for each base, which splits the triangle into congruent areas, is concurrent. The three figures below show "half a triangle" area for each base, with the segments for all three bases in place. As seen in the figures, the segments are not concurrent and are not concurrent for any case.
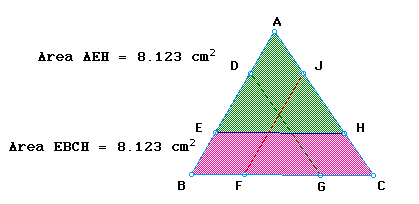
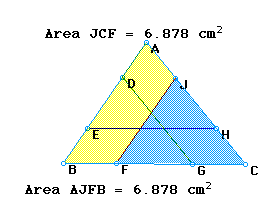
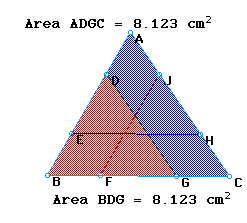
An approach here that might be considered is to have the students make a conjecture about the concurrency of the segments before viewing. One could have them make conjectures for when triangle ABC is acute, right, and/or obtuse.
FINAL DISCUSSION: Relevance of the inner triangle.
Once students discover that the segments are not concurrent, then you could move on to make conjectures about the triangle formed by the segments. Many students may realize quickly that the triangle would be similar to the other triangles , but could be prompted further to make proofs of why they are similar.
One possible Proof of the similarity:
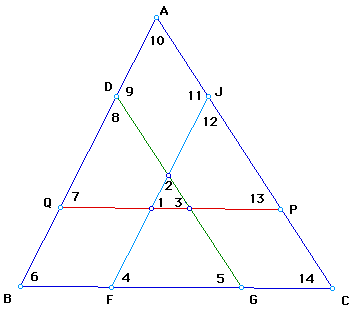
Since QP is parallel to BC, then angle 1 is congruent to angle 4. Also, since JF is parallel to AB, then angle 4 is congruent to angle 6. Therefore, by the transitive property of congruence, angle 1 is congruent to angle 6.
Since DG is parallel to AC, angle 2 is congruent to angle 11 and since JF is parallel to AB, angle 11 is congruent to angle 10. Again by the transitive property of congruence, angle 2 is congruent to angle 10.
Continuing, since DG is parallel to AC, angle 3 is congruent to angle 12 and with QP being parallel to BC, then angle 12 is congruent to angle 14 and by the transitive property of congruence, angle 3 is congruent to angle 14.
By AAA, the inner triangle is similar to triangle ABC and to the triangles formed by the segments bisecting the area.