A. The following is an exploration, proof, and simulation of any triangle ABC and an interior point P where segments

AP, BP, and CP extend to the intersections of the opposite sides of the triangle.

The figure below shows the set-up.

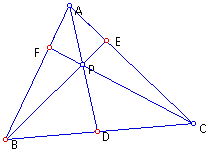
B. After some exploration of the above figure, the conclusion can be made that (AF)(BD)(EC) is always equal to

(FB)(DC)(EA) for various triangles and various locations of P.

In Dr. Wilson's "Exploration of A Triangle Ratios Problem", I gather that using parallel lines to find similar

triangles should help with the proof of the above conjecture. The figure below shows parallel lines through points

B and C of the triangle ABC.

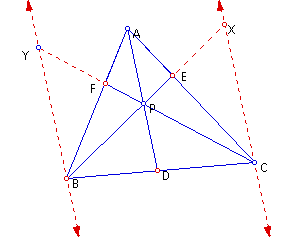
The triangles are similar by AA or by SAS similarity postulates:

Here are the proportions for each triangle listed above:

1. AFP and BFY

2. AEP and CEX

3. YBC and PDC

4. PDB and XCB

Using these proportions, I will focus primarily on the following four:

1.

2.

3.

4.

When taking the proportions above and multiplying 1, 3, and 4 downward, I get the following:

Upon simplifying the above, this yields:

I also know

and so by substitutions I now have

Next, by multiplying both sides of this equation by

the result is

and thus

Reference

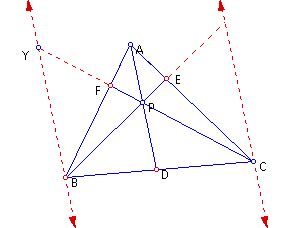
The image and calculations show below are the basis for the direction of this proof. Upon exploring and manipulating the triangle, I noticed that the product of the ratiosalways held to equal to .

With further study of the ratios and the given values for this particular triangle, the following ratios when multiplied

together will equal the ratio EA/CE, shown below. I viewed numerous locations of P and this held.

C. The information that is linked to sketchpad discusses how the ratio of the area of triangle ABC compares to the

ratio of the area of triangle DEF.

Return