Assignment 9: Petal Triangles
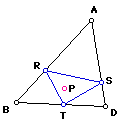
Let triangle ABC be any triangle. Then if P is any point in the plane, then the triangle formed by constructing perpendiculars to the sides of ABD ( extended if necessary) locate three points R, S, T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P.

So, now we have a petal triangle.
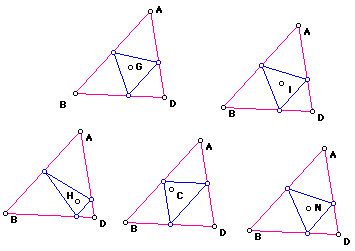
We can look at the petal triangle if the petal point is the centroid, incenter, orthocenter, circumcenter and center of the nine point circle for triangle ABD.
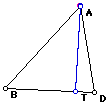
Next, let's look at an instance when the petal point is a point on the side of the triangle ABC.
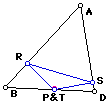
Note that the petal triangle becomes a degenerate triangle when P is one of the vertices of triangle ABD. This means that the three vertices of the Pedal triangle are colinear.
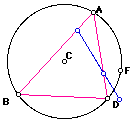
Now we can find all conditions in which the three vertices of the Pedal triangle are colinear. This line segment is called the Simson Line. We can note that the Simson Line is formed when ever the petal point is located on the circumcircle of the original triangle. In this example point F is the petal point.
Locate the midpoints of the sides of the Pedal Triangle. Trace the locus of the midpoints of the sides of the Pedal Triangle as the Pedal point is animated around the circumcircle. Notice that three ellipses are formed.

We can also trace the lines formed from the sides of the Pedal triangle as the Pedal point is moved around the circle.

Note that it is interesting to look at the different situation of the Pedal point being annotated arounde larger and smaller circles.