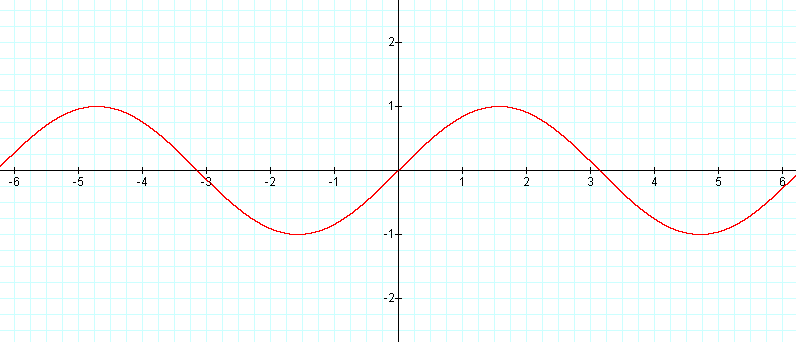
To examine the graph of y = sin x, I will examine y = A sin (Bx +C) for different values of A, B, and C. This will allow me to make a generalization for the values of A, B, and C and thus will know how to graph a function of y = sin x quickly.

Let's us first look at the graph y = sin x. This is were A and B equal 1 and C equals 0. This is the graph that we will compare other graphs to.

y = sin x

y = 2sin x

y = 3sin x

y = -sin x

y = -2sin x

y = -3sin x

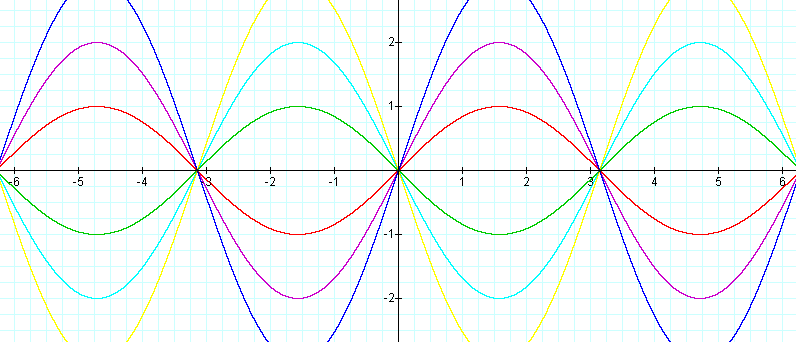
We can see from the graph above what the differences are when we change the value of "A" in y = A sinx. Notice that the magnitude of the curves is what is affected. This is called the amplitude of the curve. So A affects amplitude. To figure out the amplitude of a curve we can use this easy formula.

Now that we know what the magnitude of the amplitude is, we need to decide if the sign of A is of any importance. Notice that the last three graphs are negative values for A. Does this make a difference? We can see that they reflect the graphs with the same numerical values (only positive) about the x-axis.

y = sin x

y = sin (2x)

y = sin (3x)

y = sin (-x)

y = sin (-2x)

y = sin (-3x)

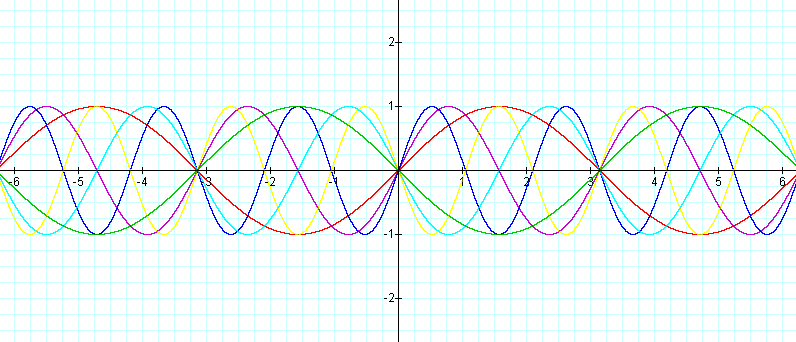
It appears that B affects the period of the curve. To see if this is true, lets graph some curves where the value of B is less than zero.

y = sin x

y = sin (1/2 x)

y = sin (1/3 x)

y = sin (-x)

y = sin (-1/2 x)

y = sin (-1/3 x)

We can see that in fact, B does affect the period of the curve. It takes 1/B times to complete a period of a curve. If B is equal to 1, then it takes 2pi to complete a period. If B is equal to 2, then it takes only pi to complete a period. If B is equal to 1/2, then it takes only 4pi to complete a period, twice as long as a normal period. Once again we see that the negative only causes a reflection about the x-axis.

y = sin x

y = sin (x + 1)

y = sin (x + 2)

y = sin (x - 1)

y = sin (x - 2)

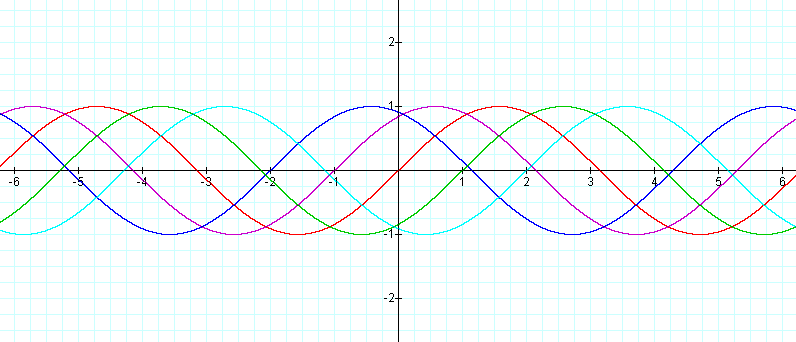
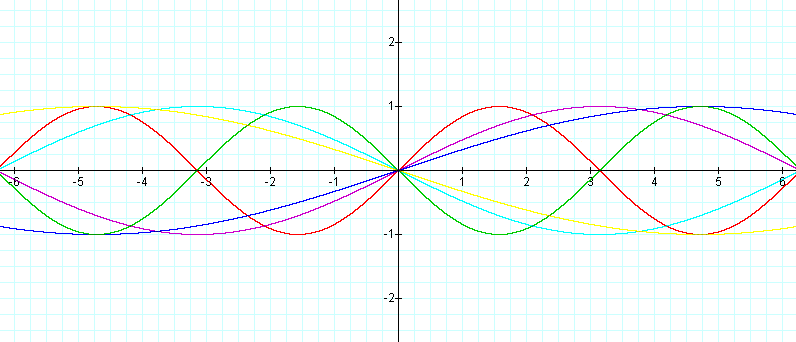
Automatically we can see that the actual picture of the graph does not change, it only shifts. If C is positive it shifts to the right, if C is negative it shifts to the left. Thus C affects the horizontal displacement (or shift) of the graph.