It has now become a rather standard exercise, with available technology,
to construct graphs to consider the equation
and to overlay several graphs of
for different values of a, b, or c as the other two are held constant.
From these graphs discussion of the patterns for the roots of
can be followed. For example, if we set
for b = -3, -2, -1, 0, 1, 2, 3, and overlay the graphs, the following
picture is obtained.
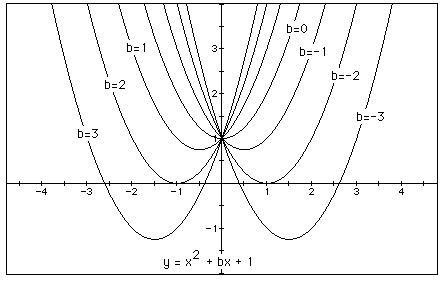
We can discuss the "movement" of a parabola as b is changed.
The parabola always passes through the same point on the y-axis ( the point
(0,1) with this equation). For b < -2 the parabola will intersect the
x-axis in two points with positive x values (i.e. the original equation
will have two real roots, both positive). For b = -2, the parabola is tangent
to the x-axis and so the original equation has one real and positive root
at the point of tangency. For -2 < b < 2, the parabola does not intersect
the x-axis -- the original equation has no real roots. Similarly for b =
2 the parabola is tangent to the x-axis (one real negative root) and for
b > 2, the parabola intersects the x-axis twice to show two negative
real roots for each b.
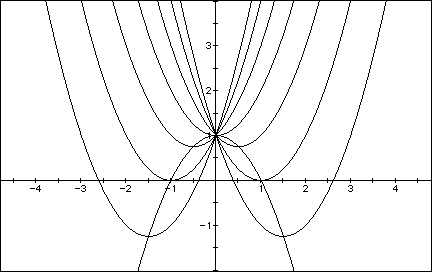
Now consider the locus of the vertices of the set of parabolas graphed from
Show that the locus is the parabola
Generalize.
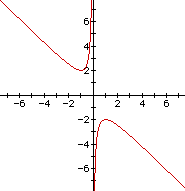
Consider again the equation
Now graph this relation in the xb plane. We get the following graph.
If we take any particular value of b, say b = 5, and overlay this equation
on the graph we add a line parallel to the x-axis. If it intersects the
curve in the xb plane the intersection points correspond to the roots of
the original equation for that value of b. We have the following graph.
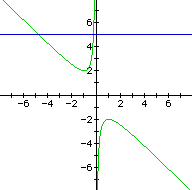
For each value of b we select, we get a horizontal line. It is clear
on a single graph that we get two negative real roots of the original equation
when b > 2, one negative real root when b = 2, no real roots for -2 <
b < 2, One positive real root when b = -2, and two positive real roots
when b < -2.
Consider the case when c = - 1 rather than + 1.
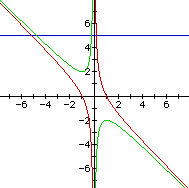
Here we can see that we get two real roots for any value of b.
In the following example the equation
is considered. If the equation is graphed in the xc plane, it is easy
to see that the curve will be a parabola. For each value of c considered,
its graph will be a line crossing the parabola in 0, 1, or 2 points -- the
intersections being at the roots of the original equation at that value
of c. In the graph, the graph of c = 1 is shown. The equation
will have two negative roots -- approximately -0.2 and -4.8.
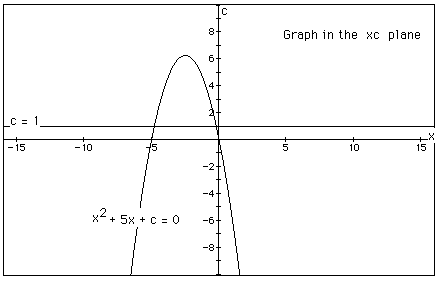
There is one value of c where the equation will have only 1 real root
-- at c = 6.25. For c > 6.25 the equation will have no real roots and
for c < 6.25 the equation will have two roots, both negative for 0 <
c < 6.25, one negative and one 0 when c = 0 and one negative and one
positive when c < 0.
Why this method while teaching?
It is obvious that this method is a little different than most teachers may like to use in their classroom. The idea of a xb or xc plane is quite different than the standard xy plane. The first reason I like this method for teaching about roots is that it is a different twist. I have found in my short study of mathematics that the world and mathematics is ever changing. I feel like teachers should teach students to look and evaluate from many different angles. Not making a judgment from one observation is a skill that all would benefit from. I think by looking at the same general equation from different planes is one way to show this life skill.
Another benefit of this approach is that the students begin to develop the purpose of constants. The students know that in the xy plane y is a function of x. Now when we look at the xb plane we see b as a function of x. But if b was 2b or 3b or some multiple of b we would see that our graph would change depending on the value of b. This will help in developing the students understanding of coefficients in quadratics.
To use this method in the classroom I would suggest the following. First, let students solve the equation for b or c depending on which plane they will be graphing in. This could be done by hand. Then allow students to use a graphing program for the computer or a graphing calculator to examine graphs of their equations. Note: When graphing b = x it should be entered as y = x. The y axis is now the b axis.