Laura
Dickerson's Assignment 9: Pedal Triangles
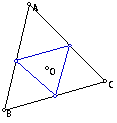
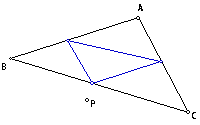 Let triangle ABC be any triangle.
Then if P is any point in the plane, then the triangle formed by constructing
perpendiculars to the sides of ABC (extended if necessary) locate three
points R, S, and T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P.
Let triangle ABC be any triangle.
Then if P is any point in the plane, then the triangle formed by constructing
perpendiculars to the sides of ABC (extended if necessary) locate three
points R, S, and T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P.
Click here for a GSP script for the general construction of a
pedal triangle to triangle ABC where P is any point in the plane
ABC.
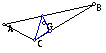
Let's suppose that pedal point P is the centroid
of triangle ABC. The following is observed:
Two vertices are always on one side
of triangle ABC.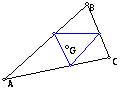
Here are a few examples.
|
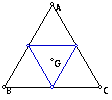
When triangle ABC is an equilateral triangle,
the pedal triangle is the medial triangle of triangle ABC.
|
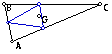
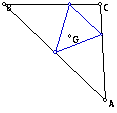
When triangle ABC is an isoceles
triangle so is the pedal triangle.
  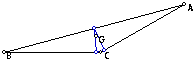
|
Let the incenter of triangle ABC be the pedal
point.
Two observations can be made. First, the pedal
triangle is always inside triangle ABC. Click
here to try to find a counter example.
Second, just like the centroid, when triangle
ABC is an isoscoles triangle so is the pedal triangle. Click
here for a GSP sketch.
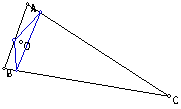
What if the pedal point is the orthocenter
of triangle ABC?
When a point is an orthocenter of a triangle
it will either be inside the triangle or outside. What we notice is that
the pedal triangle does the same as what the orthocenter or pedal point
does.
So why does this happen?
The pedal triangle is constructed by taking
the perpendiculars from point P to the sides of the triangle. Where
those lines intersect is where the vertices of the pedal triangle are.
The orthocenter is the intersection point of the three altitudes of the
triangle. An altitude is the perpendicular to a side from the opposite
vertex. So the lines that are perpendicular from the pedal point P
are the lines in which the altitudes are contained. Thus if the altitude
goes outside of the triangle (which is the case when the orthocenter is
outside of the triangle) then the pedal triangle will be outside of the
triangle.
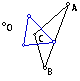
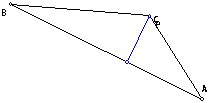
The circumcenter as the pedal point, I believe
makes the most interesting observations.
First, the pedal triangle is ALWAYS the medial
triangle of triangle ABC. I first noticed this by observation. I then measured
the distances and found that the vertices of the pedal triangle were in
fact the midpoint of the segments that formed triangle ABC. Click here for the GSP sketch that shows this. The
reason for this is that the circumcenter equidistant from each side of
the triangle. That means that it lies on the perpendicular bisector of
each side. So when one drops the perpendicular to each side of the triangle
from the circumcenter, it intersects the triangle at the midpoints. Thus
forming the medial triangle.
Second, when the circumcenter or pedal point
lies outside of triangle ABC, it passes through a vertex of the pedal point
to go on the outside. Click here to try
it out on the GSP sketch. Unfortunately I am not sure why this is true
at this time.
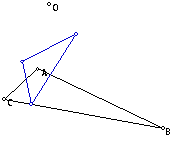
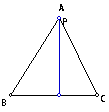
When the pedal point is on a
side of the original triangle ABC, then it acts as a vertex of the pedal
triangle. This is best illustrated by the GSP
animated sketch.
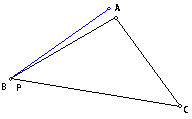
When the pedal point is one of the vertices
of the triangle then a straight line is formed. It is actually the altitude
from that vertex to the opposite side.
 Let triangle ABC be any triangle.
Then if P is any point in the plane, then the triangle formed by constructing
perpendiculars to the sides of ABC (extended if necessary) locate three
points R, S, and T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P.
Let triangle ABC be any triangle.
Then if P is any point in the plane, then the triangle formed by constructing
perpendiculars to the sides of ABC (extended if necessary) locate three
points R, S, and T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P.