Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.
First let's look at some examples:
Just from these examples we can not conclude that our conjecture that the ration of the measurements is equal to one is true. As of right now it appears that this is true. Click here for a GSP sketch of this triangle with the movable point P. |
Conjecture? Prove it! My conjecture is stated above: Given any triangle ABC and any point P (inside or outside of triangle), the following can be observed. After constructing lines AP, BP, and CP and extending the lines to intersect the opposite side of the triangle at points D, E, and F respectively, the following ratio holds for all cases. 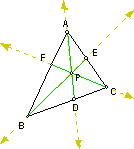
We can see right away that there are many congruent angles thus letting us see many similar triangles. They key is to find the similar triangles that give us the proportion we need to prove that our ratio is indeed 1. Using the previous triangles, we shall now see that corresponding parts are also similar and look at the following. Now let us look at these proportions to see that the ratio does equal 1. 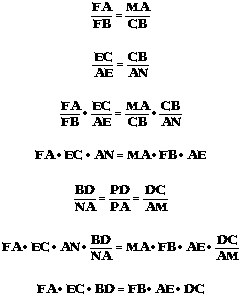 Thus we can see that the conjecture is true. What is surprising interesting is that it really does not matter where point P is (inside or outside of the triangle). Click here to go back to the GSP sketch and try for yourself. |
Show that the ratio of the areas of ABC and DEF is always greater than or equal to 4. When is it equal to 4? 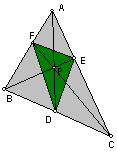 To investigate this part of the project, I will use Geometer's Sketch Pad. If we look at the GSP sketch it is easy to see that the ratio will always be greater than or equal to 4 (if the point P is inside the triangle). The real task is to find out when the ratio will be exactly 4.
My first theory is to look at the properties of the triangle. Let see if for a special triangle the ratio is 4. I looked at an equilateral triangle. I found that this did not get me anywhere. I needed to focus on the point P.
I then looked at different distinct point that lie inside the triangle. I looked at the incenter, orthocenter, circumcenter and centroid for the triangle ABC. I found that all four "centers" would let the ratio be 4 in an equilateral triangle. I would then have to test it for any triangle. After I tested this, I found that only when point P is the centroid, the ratio of the areas is 4. |
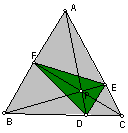
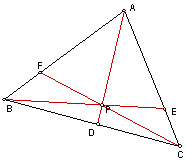 Consider any triangle
ABC. Select a point P inside the triangle and draw lines AP, BP, and CP
extended to their intersections with the opposite sides in points D, E,
and F respectively.
Consider any triangle
ABC. Select a point P inside the triangle and draw lines AP, BP, and CP
extended to their intersections with the opposite sides in points D, E,
and F respectively.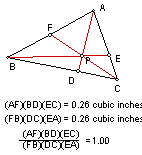
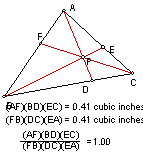
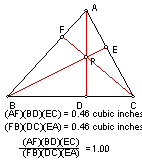
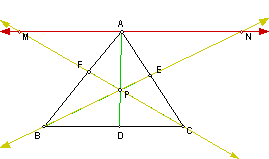 Let us start our proof
by looking at what happens if we extend segment BE and CF. Mark the points
M and N where they intersect the line through A which is parallel to segment
BC.
Let us start our proof
by looking at what happens if we extend segment BE and CF. Mark the points
M and N where they intersect the line through A which is parallel to segment
BC.