Day 1 Distance of a segment

objectives:

(1) to define abscissa and ordinate

(2) to find the length of a line segment

In coordinate geometry, familiar geometric ideas are expressed in terms of numbers.Each point of a plane is associated with an ordered pair of real numbers, called coordinates of a point. Also, each ordered pair of real numbers is associated with a point of the plane. This idea is illustrated in the diagram.

As illustrated in the diagram, the x- and y-axes separate the plane into four regions, called quadrants, which are numbered I, II, III, IV, as shown. The x-coordinates are known as the abscissa and the y-coordinates are known as ordinates.

In the first section, we will see how numbers can be used to express the distance between two points and describe the midpoint of a line segment.

The distance between two points A and B will be denoted by AB. . To find the distance AB, horizontal and vertical lines are drawn through A and B to form a right triangle. The horizontal distance AC is found by calculating the absolute value of the difference of the x-coordinates of C and A. The vertical distance BC is found by calculating the absolute value of the difference of the y-coordinates of B and C. Then the Pythagorean Theorem is used.

and The use of the Pythagorean Theorem yields:

for the figure above. illustrates the same idea for two arbitrary points, (X1,Y1) and (Y1,Y2).This equation is known as the distance formula; it is a tool which allows you to calculate and compare distances. You may find it easier to remember this formula by visualizing the diagrams above and using the Pythagorean Theorem.

Day 2 Midpoint of a segment

objectives:

(1) to find the midpoint of a line segment

What are the coordinates of the midpoint M on the segment AB shown in figure (a) below?

figure (a) figure (b)

Figure (b) shows that the x-coordinate of M is 3=(1+5)/2, the average of 1 and 5. Likewise, figure (c) shows that
the y-coordinate of M is 4=(2+6)/2, the average of 2 and 6.

A generalization of this reasoning is shown below. In the diagrams the x- and y-coordinates of the midpoint are denoted by x and y.

Summary
In coordinate geometry, familiar geometric ideas are expressed in terms of numbers. A point in the plane is identified with a pair of numbers called its coordinates. Moreover, if A=(X1,Y1) and B=(X2,Y2) are two points of the plane, then the length and midpoint of AB can be expressed in terms of numbers by the following formulas:

Distance formula:

Midpoint formula:

Day 3 Linear Equations

objectives:

(1) to use algebraic equations to describe lines

A solution of the equation 2x + 3y = 12 is an ordered pair of numbers (x , y) which makes the equation true. For
example, since x = 0 and y = 4 make the equation true, the pair (0 , 4) is a solution. Another solution is (-3 , 6)
because 2(-3) + 3(6) = 12. The set of all points in the plane corresponding to ordered-pair solutions of the
equations is called the graph of the equation.

The equation 2x + 3y = 12, whose graph we have just considered, is one of the simplest kinds of equations in two
variables. The graph of any equation having the form ax + by = c is often referred to as the line "ax + by = c."

There are many different linear equations which have the same graph. All these equations are related to each other by simple algebraic transformations. For example, the equations 4x - 2y = 2, 2x - y = 1, and y = 2x -1 all have the same graph. Of these three equations, the last one is most useful for making a table of points for the graph.

x	y = 2x - 1
0	-1
1	1
2	3
3	5

If a = 0 or b = 0, the equation ax + by = c looks strange. Consider for example, the equation y = 4. This looks like a
statement that some number y equals 4. But it really refers to the set of ordered pairs (x ,y) for which y = 4. Its
graph is shown below. Likewise, the graph of x = 2, also shown below, consists of all ordered pairs (x , y ) for
which x = 2.

You can find the intersection of two lines geometrically by plotting their graphs. In this section you will see how
the intersection can be found algebraically. Consider the following pair of equations:

3x + 2y = 12
-4x + 5y = 15

The graphs of both equations are straight lines which intersect in a point. To find this point, we solve the equations
simultaneously. One method of doing this is to multiply both sides of the first equation by 4 and both sides of the
second by 3, obtaining the following equations:

3x + 2y = 12
-4x + 5y = 15
y = 93/23

In a similar manner, we find that x = 30/23. Thus, (30/23 , 93/23) is the common solution of the two linear
equations. It is also the point common to their graphs.

However, two lines in a plane do not have to intersect. For example, the equations

6x + 4y = 8
3x + 2y = 1

have parallel line graphs. If you try to solve these equations simultaneously, you will find that they contradict
each other and therefore have no common solution.

A slight modification of the previous two equations gives us a different geometric picture. Consider the following
linear equations:

6x + 4y = 8
3x + 2y = 4

These equations have an infinite number of common solutions, and their graphs are the same line.

Day 4 The Slope of Lines

objectives:

(1) to find the slope of lines

In geometry we can prove that two lines L1 and L2, are parallel by proving that a pair of corresponding angles are congruent. It is a weakness of coordinate geometry that these angles cannot be evaluated easily. However, there is a concept in coordinate geometry that describes the steepness of a line relative to the x-axis. It is called slope, and we shall see that the lines L1 and L2 can be proved parallel by showing that they have the same slope.

The slope of a nonvertical line through the points (X1,Y1) and (X2,Y2) is defined by the equation

Thus, to determine the slope of a line, choose any two points on the line, for instance, (2,0) and (5,6) in figure (a) below. Subtract the y-coordinates, 6-0=6, and also the x-coordinates, 5-2=3. The ratio of these numbers, 6/3 = 2, is the slope. Notice that if you consider two other points, (-1,-6) and (0,-4), you get the same value for the slope.

Now let us imagine the line in figure (a) rotating counterclockwise about the point (2,0). In figure (b), you see that as the line becomes steeper, its slope gets very large. In fact, when the line is vertical, as in figure (c), it is so steep that some people say that the line has infinite slope, although it is really more precise to say that it has no slope because the denominator is zero.

If you imagine the line rotating still more about (2,0), you will see that the slope becomes negative. (See figure (d) and (e).) The horizontal line through (2,0) has slope zero. (See figure (f).) Note that "zero slope" and "no slope" mean different things, as the diagram illustrates.

The following theorem proves that the slope (Y2-Y1)/(X2-X1) is the same for any two points of a line. It also provides an easy way way to find the slope of a line from its equation.

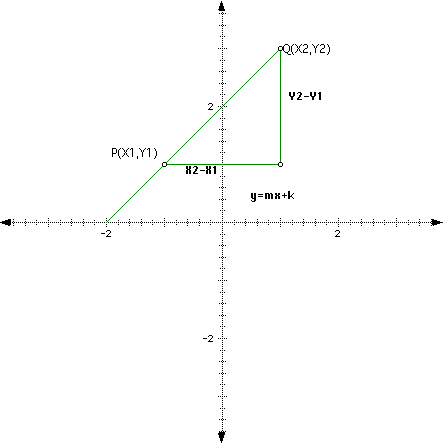
Theorem: The slope of the line with equation y = mx + k is m.

Proof: Let P = (X1,Y1) and Q = (X2,Y2) be any two different points of the line with equation y = mx + k. Then Y1 = mx + k and Y2 = mx + k. Therefore, the slope equals

(Y2-Y1) / (X2-X1) = (mX2 + k) - (mX1 + k) / (X2 -X1) =

m(X2 - X1) / (X2 - X1) = m.

When the equation of a line is written in the form y = mx + k, the numbers m and k should provide you with a mental picture of the line. According to the theorem, m is the slope of the line. The number k is called the y-intercept of the line because the line intersects the y-axis at the point (0,k). The diagrams below illustrate the effect of m and k on the graph of the equation y = mx + k. Notice in the diagram that lines with the same slope are parallel.

Given the equation 7x + 13y = 26, find the slope and y-intercept of the line.

Solution: First rewrite the equation as follows:

The slope is then -7/13, the coefficient of x. The y-intercept is 2.

In general, if the equation of a line is written in the form

ax + by = c, then the slope m of the line is -a/b and its y-intercept k is c/b.

Day 5: Parallel and Perpendicular Lines

objective:

(1) to show how the slope is related to the geometric ideas of parallel and perpendicular lines

In our development of coordinate geometry, we have shown how algebraic relationships involving numbers are used to describe geometric relationships involving points and lines.

Algebraic Idea	Geometric Idea
An ordered pair of numbers (x,y)	A point in the plane
An equation ax + by = c (a and b not both 0)	A line in the plane
Solution of two linear equations	Point common to two lines
The number (Y2-Y1)/(X2-X1)	Slope of the line joining two points (X1,Y1) and (X2,Y2)
The number	Distance between points (X1,Y1) and (X2,Y2)
An ordered pair of numbers	Midpoint of segment joining points (X1,Y1) and (X2,Y2)

We shall extend these lists by proving two theorems which show how the slope is related to the geometric ideas of parallel and perpendicular lines.

Theorem1:

a. If two nonvertical lines are parallel, then they have the same slope.

b. If two (different) nonvertical lines have the same slope, then they are parallel.

Proof: Suppose L1 and L2 are nonvertical lines as shown. Note that the slope of L1 is BC/AC and the slope of L2 is EF/DF.

A. 1. Suppose L1 is parallel to L2.

2. Then <BAC and <EDF are congruent.

3. Triangle ABC is similar to triangle DEF.

4. Thus, BC/AC = EF/DF.

5. That is, the lines have equal slopes.

B. 1. Suppose the lines have equal slopes, that is BC/AC= EF/DF.

2. Then triangle ABC is similar to triangle DEF.(SAS)

3. Thus, <BAC and <EDF are congruent.

4. Therefore, L1 and L2 are parallel.

In coordinate geometry it is sometimes convenient to consider coincident lines to be parallel. If this is done, then the word "different" can be omitted from part (b) of Theorem 1.

Since vertical lines have no slope, they are not included in Theorem 2 which follows. Note, however, that any two (different) vertical lines are parallel and any vertical line is perpendicular to any horizontal line.

Theorem 2: Given two lines with slopes M1 and M2:

A. If the lines are perpendicular, then M1 = -1/M2.

B. If M1 = -1/M2, then the lines are perpendicular.

Proof: Suppose L1 and L2 are nonvertical lines intersecting at O. The dotted lines shown are horizontal and vertical, so that the angles are right angles. Note that M1 = AB/BO and M2 = DO/-CD.

A. 1. Suppose L1 is perpendicular to L2, so that <COA is right.

2. Then <AOB =<COD since both are complements of <DOA, and

3. Triangles AOB and COD are similar.(AA similarity)

4. Thus AB/BO = CD/DO. That is, M1 = -1/M2.

B. 1. Suppose M1 = -1/M2. That is, AB/BO = CD/DO.

2. Thus triangles AOB and COD are similar. (SAS similarity),and

3. <AOB = <COD.

4. Hence <COA is a right angle because of Step 3 and the fact that <DOB is a right angle. Hence L1 and L2 are perpendicular.

Day 6: Finding Equations of Lines

Objective:

(1) to find the equation given a line

In the text and exercises of this section, we shall be concerned with finding an equation for each of these lines.

1. The line through a given point with a specified slope.

2. The line through two given points.

3. The perpendicular bisector of a segment.

In the following three examples, we shall find equations for the list above.

Example 1: Write an equation of the line through the point (5,2) with slope 3.

Solution: Let (x,y) be a point on the line. Since the slope is 3, we have

Although this equation can be simplified to y= 3x - 13, or 3x - y = 13, the original form (Y-2)/( X-5) = 13 is easy to remember when you think of the picture shown. All nonvertical lines through (a,b) have an equation of the form

where m is the slope of the line. The vertical line through (a,b) has equation x = a.

Example 2: Write an equation of the line through (-3,4) and (2,5).

Solution: First find the slope of the line:

Both of these will yield the equation 5y - x = 23.

Example 3: Write an equation of the perpendicular bisector of the segment joining A = (-2,3) and B=(4,-5).

Solution:

1. Since the slope of AB is -5-3 / 4-(-2) = -4 / 3, the slope of the perpendicular bisector is the negative reciprocal of -4 / 3, namely 3 / 4.

2. The perpendicular bisector must pass through the midpoint of AB. Using the midpoint formula, this is the point

3. The equation of the line through (1,-1) with slope 3 / 4 is

which can be simplified to 3x - 4y = 7.

Day 7 Unit Review

objectives:

(1) to play "jeopardy" as a review for the objectives of the unit

MATH JEOPARDY

This game is a variation of the popular television show "Jeopardy." All you need to play this game is a basic understanding of the television show, six sheets of each of five colors of construction paper, a marker, and a chalkboard. This game is ideal for any math class in middle school or high school. It takes about 20 minutes of teacher preparation time and at least 30 minutes to play. It can even be continued to another day if you need to stop play in the middle of a game.

To prepare, the teacher selects five categories and 'Writes five questions for each category. The questions should be of varying difficulty in each category.

Write each category name on a different color of construction paper and tape it to the board with one row at the top of the board. Use the remaining paper to write questions on one side of the paper and a dollar amount on the other side. Be sure to use the same color of paper for questions in the same category Tape these, with the dollar amounts showing, in columns under the category headings making a grid of solid colored columns. Make sure the dollar amounts are in increasing order. The game board is now ready for play.

To begin play, separate the class into two teams of students of equal ability. The groups then choose a captain and they also select a name. Write the name of each team on the board. Use these to keep score. After deciding which team goes first, the captain of that team selects a team member to start play for that team. The team member selects the category and dollar amount for the question. The teacher reads the statement after turning over the dollar card from the board. The student, without any help from teammates, has a specified amount of time to answer. If he or she answers it correctly, then the captain selects a second team member to go next. This team member also selects the dollar amount and the category for his or her question and play proceeds as before. The maximum number of consecutive correct responses for one team is three and then play goes to the other team for the same number of consecutive correct responses. However, if a person misses a question, then the question goes to the other team, whose members may confer and answer. If the answer is correct, that team begins its turn and the other team loses its turn. If the conferring team misses the question, play goes back to the original team. That team starts fresh with another turn and play continues.

To keep track of-the scoring, place the paper with the dollar amount on it under the name of the team on the board and keep a running total of dollars from both teams.

After all questions have been answered and scores totaled, "final jeopardy" is started by announcing the category. Each team then confers for one minute to decide the amount of its wager. They- must write the wager down on paper and put it on the board by the team total. The question is then read and the teams are given one minute to write their answers and give it to the captain. The teacher reads each answer and totals the scores. (Add a drum roll or two for dramatic effect!) The game is over and the winners are announced and congratulated.

Day 8 Unit Exam

objectives:

(1) to satisfy the objectives of the unit

Equations

1. a. Can the expression ever be negative? Can it ever be zero?

b.Is the distance between two points ever negative? Under what special circumstance can the distance between "two" points be zero?

2. Plot the points A = (-3,1), B = (-3,7), and C - (5,4), and use the distance formula to show that triangle ABC is isosceles.

3. Give the coordinates of three points each equidistant from R = (1,8) and S = (5,8).

4. a. All points on the x-axis have one of their coordinates zero. Which coordinate?

b. All points on the y-axis have one of their coordinates zero. Which coordinate?

5. Give the coordinates of the points where the graph of 3x - 2y = 12 intersects the x-axis and the y-axis.

6. In one drawing, sketch the horizontal line through (2,3) and the vertical line through (5,-1). What is the intersection point of these lines? What are the equations of these lines?

7. Estimate the common solution of the equations 3x - 4y = 8 and 4x + 5y = 15. Check your estimate by solving the equations simultaneously.

8. Give equations of two lines which are parallel to the line 7x - 4y = 12.

9. Find the slope for the points (-3,1) and (3,-5).

10. What is the slope of a horizontal line?

11. Explain why a vertical line has no slope.

12. Write an equation of the line with slope 5 and y-intercept 6.

13. A line L has slope 2/3. What is the slope of a line (a) parallel to L, (b) perpendicular to L?

14. A line L has equation 8x - 5y = 7. What is the slope of a line (a) parallel to L, (b) perpendicular to L?

15. Find the value of h if the line joining (2,h) and (4,9) and the line y = 3x + 4 are (a) parallel, (b) perpendicular.

Write and equation of the line described.

16. The line through (-1,-3) with slope 5.

17. The line through (-1,4) and (5,8).

18. The line through (-1,2) parallel to the line 3x + 4y = 1.

19. The line through (6,2) perpendicular to the line 7x + 4y = 8.

20. A horizontal line through (2,3).

Day 9: Extension

(1) to find patterns in the graphs of linear equations

Exploration 2.2 Deducing Functional Formulas from Data

EXPLORATION 2.2

Deducing Functional Formulas from Data

Objectives

· find and describe patterns in data

* deduce functional formulas from data tables

· extend patterns using functional formulas

Materials/Equipment

none required

Procedure

Class discussion

0 Examine the following data table. Look for a pattern in terms of how y changes

when x changes. Explain in your own words how to find y in terms of x.

x y x y

0 0.0 0 5

1 0.5 1 8

2 1.0 2 11

3 1.5 3 14

4 2.0 4 17

· Assume that the pattern continues indefinitely, use the rule you have found to extend the data table to include negative numbers for x.

· Check your extended data tables. Did you find a unique value for y given a particular value for x?

· Use a formula to describe the pattern that you have found. Do you think this formula describes a function? Explain.

On your own

Use the following data tables to explain in your owns words how to find y in terms of x and extend each of the data tables using the rule you have found.

Use a formula to describe the pattern that you have found.

x y x y x y

0 0 0 0 0 0

1 1 1 1 1 2

2 4 2 8 2 12

3 9 3 27 3 36

4 16 4 1 64 4 80

Exploration 2.2 Deducin@Functional Formulas from Data

x	y	x	y	x	y
-2	0	0	-1	0	3
0	10	1	0	10	8
5	35	2	3	20	13
10	60	3	8	30	18
100	510	4	15	100	53

Discussion/Analysis

With a partner:

Compare your results. Do the formulas that you have found describe functions?

Explain.

Class Discussion

Does the rest of the class agree with your results? Remember that formulas that look different may give the same results.

Exploration Linked Homework

1 a) For each of the following data tables, explain in your own words how to find y in

terms of x. Using the rule you have found, extend each of the data tables to include negative numbers.

x y x y

-10 10.0 0 -3

0 0.0 1 1

3 0.9 2 5

8 6.4 3 9

10 10.0 4 13

b) Use a formula to describe the pattern you have found. Does your formula describe a function? Explain.

2. Make up a functional formula, generate a data table and bring the data table on a separate piece of paper to class. The class will be asked to find your rule and express it as a formula.

3. A graduated income tax is proposed in Borduria to replace an existing flat rate of 8% on all income. The new proposal is that persons will pay no tax on their first $20,000 income, 5% on their income over $20,000 to $100,000, and 107o on their income over $100,000.

a) Construct a table of values that shows how much tax persons will pay under both the existing 8% flat tax and the proposed new tax for each of the following in-

comes: $0, $20,000; $50,000; $100,000; $150,000; $200,000.

b) Placing income on the horizontal axis, construct a graph of tax dollars vs. income for the 8% flat tax.

c) On the same graph plot tax dollars vs. income for the proposed new graduated tax.

d) Construct a function that describes tax dollars under the existing 8% tax as a function of income.

e) Construct a piecewise function that describes tax dollars under the proposed new tax rates as a function of income.

f) Use your graph to estimate income level for which the taxes are the same under both plans. What plan is best for those below this income? For those above this income?

Use your equations to find the coordinates that represent the point at which the taxes are the same for both plans. Label this point on your graph.

h) If the median income in the state is $27,000 and the mean income is $35,000, do you think the new graduated tax would be voted in by the people?

Note: (Borduria is a fictional totalitarian state in the Balkans that figures in the adventures of TinTin.)

4. Heart health is a prime concern, because -heart disease is theleading cause of death in the U.S. Aerobic activities like walking, jogging, and running are recommended for cardiovascular fitness, because they increase the heart's strength and stamina.

a) A typical training recommendation for a beginner is to walk at a moderate pace of about 3.5 miles per hour for 20 minutes. Construct a function that describes the distance traveled (D beginner), as a function of time, T, in minutes, for someone maintaining this pace. (Hint you need to convert the pace into miles per minute.) Construct a small table of solutions and graph the function, using a reasonable domain.

b) A more advanced training routine is to walk at a pace of 3.7,5 miles per hour for 10 minutes, and then jog at 5.25 miles per hour for 10 minutes. Construct a piecewise linear function that gives the total distance (D advanced), as a function of time, T, in minutes. Generate a small table of solution and add the graph of this function to your graph in part a).

c) Do these two graphs intersect? If so, what does the intersection point represent?

5. (Optional use of graphing calculator or computer.)

The following table shows (for years between 1965 and 1993 and for people 18 and

the total 7o of cigarette smokers; the '7o of all males that smoke: and the 7o of all females that smoke.

a) By hand, draw a scatter plot of the percentage of all current smokers 18 and older vs. time. i)Calculate the average rate of change between 1965 and 1992.

ii) Calculate the average rate of change between 1990 and 1992.

Be sure to specify the units in each case.

Year '7o of smokers, 7o total 7o total

18 and older male female

1965 42.4 51.9 33.9

1974 37.1 43.1 32.1

1979 33.5 37.5 29.9

1983 32.1 35.1 29.5

1985 30.1 32.6 27.9

1987 28.8 31.2 26.5

1988 28.1 30.8 25.7

1990 25.5 28.4 22.8

1991 25.6 28.1 23.5

1992 26.5 28.6 24.6

1993 24.2 26.2 22.3

Source: U.S. National Center for Health Statistics, Health, United States, 1993 in The American Al??ianac: Statistical Abstract of the United States, 1995.

b) On your graph, sketch in an approximate regression line. By estimating coordinates of points on your regression line, calculate the average rate of change of the percentage of total smokers with respect to time.

c) (optional) Using a calculator or computer, generate a regression line for the percentage of all smokers 18 and older as a function of time. (You may wish to set 1965 as ye ar 0, and let the independent variable represent the number of years since 1965.) Record the equation and the correlation coefficient. How good a fit is this regression line to the data? Compare the rate of change for your hand generated regression line to the rate of change for the technology generated regression line.

d) Generate and record regression lines (and their associated correlation coefficients if you are using technology), for the percentage of both male and female smokers as functions of time.

e) Write a summary paragraph using the results from your graphs and calculations to describe the trends in smoking from 1965 to 1992. Would you expect this overall trend to continue? Why?