Construct a triangle and its medians. Construct a second triangle with the three sides having the lengths of the three medians from your first triangle. Find some relationship between the two triangles.!

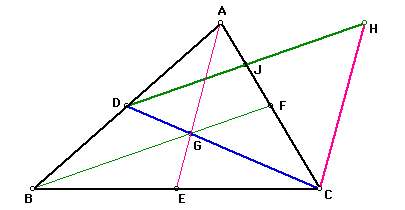
I constructed two triangles above (triangle ABC and triangle CDH), and moved some vertices and sides. I found some relationships between the two triangles ,which are unchangeble relationship anyhow I moved triangles. Among them, I try to prove following relationships.
(1)The ratio of the lemgth of segment AJ and the lemgth of
segment JC is always 0.75.
(2)The ratio of the area of triangle HDC and the area of triangle
ABCis always 0.75.
The two statements have a relation closely. When the ratio of JC : AC is 3:4, the ratio of the area HDC:the area of triangle ABC is 3:4. Considering to divide the triangle DCA by the segment DJ, the ratio of JC:AC is equal to the ratio of area DCJ : area DCA. The area of DCJ is half of HDC and the area of ADC is half of ABC. So if the ratio of JC: AC is always 3:4 (that is 0.75), the ratio of the area of triangle HDC : the area of triangle ABC is always 3:4 (that is 0.75).
prof
The ratio of the lemgth of segment AJ and the lemgth of segment
JC is always 0.75
(guideline: I prove ADFH is parallelogram, and J is the intersect point of two dialog lines and J is the midpoint of side AF. J divides AC, AJ:JC is 1:4, so JC:AC is 3:4)
Here is a triangle ABC, and given the point D, F, and C are the midpoints of the side AB, BC and CA. AD=DC, BE=EC, CF=FA.
Draw the segment BF, and DH' which is through the point D and parallel to BF. We can construct the parallelogram DBFH', so BD=FH' and BD is pallalel to FH'. So FH' is equal and parallel to AD, because AD is equal and parallel to BD, therefore ADFH' is parallelogram....(a). figure-1
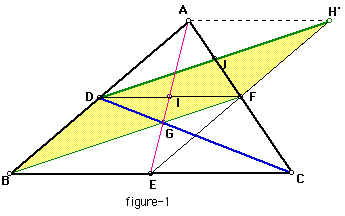
Secondly we draw another parallelogram. Draw the segment AE, and CH'' which is through the point C and parallel to AE. We can construct the parallelogram AECH'', and EC is equal and parallel to EH''. Because BE is equal and parallel to EC, ABEH is parallelogram. And ADFH'' is also parallelogram,because DF is equal and parallel to BE.....(b). figure-2
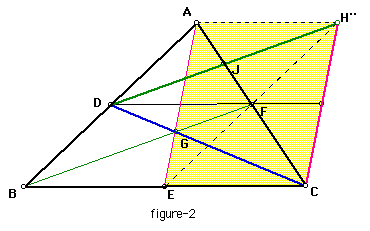
Hence Parallelogram ADFH' and Parallelogram ADFH'' are the same , and point H' and point H'' is also the same.
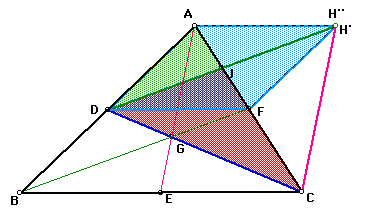
So the point J is the midpoint of side AF. J divides AC, AJ:JC
is 1:4, so JC:AC is 3:4.
Given triangle is ABC and CDH(H=H',H''), from prof above, the
area of DCJ is 3/4 of the area of ADC, so the area of HDC is 3/4
(0.75) of the area of ABC. Here is the
GSP scketch.
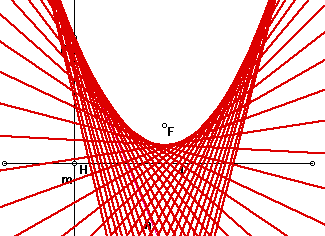
A parabola is the set of points equidistant from a line, called the directrix, and a fixed point, called the focus. Assume the focus is not on the line. Construct a parabola given a fixed point for the focus and a line (segment) for the directrix.
Draw the perpendicular line m at point H.
Connect F and H, and put the midpoint. At this point, draw the
perpendicular line n.
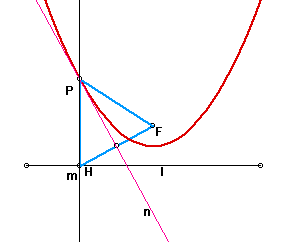
The intersected point P by line m and line n traces Parabola.
(Triangle PFH is isosceles triangle)