Given two circles and a point on one of the circles.
Construct a circle tangent to rhe two circles with one point of
tangency being the designated point.
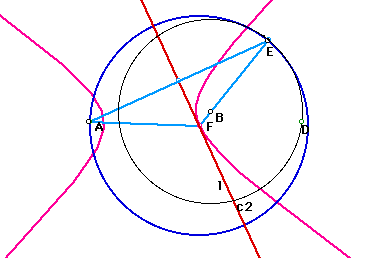
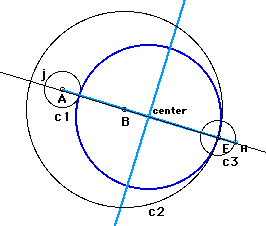
Point A is a center of the circle, point B is also a center of
the circle.
Point E is a tangent point on the circle.

The center of the desired circle will lie along a line j from
the center of the given circles with the specified point.
We need to find another locus for the center of the tangent circle.
If we add the line through the center of the desired circle and
the segment from the center of the desired circle to the center
of the second given circle c1. The segment is always of length
the sum of the radius of the desired circle plus the redius of
the given circle that didn't have a specified point. The same
distancecan be laid off along the line through the given point
from the center of the desired circle, by constructing an additional
circle c3 of the same radius with the center at the desired tangent
point E.
An isosceles triangle(center-A-H) is formed like this.
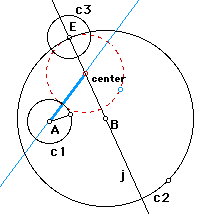
The center of the desired tangent circle lies along the perpendicular
bisector of the base of this isosceles triangle. Now we have a
construction of the desired circle.
That is, construct a line through the center of the circle with
the designated point of tangency and construct a circle of the
same radius as the second of the given circles with the designated
point as center. The intersection of the line and circle will
allow construction of the base of the isosceles triangle and hence
allow location of the center of the desired circle.
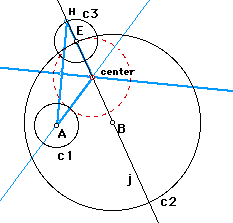
If the center of the constructed circle is connected by segments to the centers of the two given circles, it is immediate that the sum of the segments is the same as the sum of the radii of the two given circles. This the sum is a constant and therefore the locus of the centers of the tangent circles is an ellipse with foci at the centers of the given circles.
With GSP, we can animate around the circle and trace the locus of the center as follows. Here is a script of tangent circle.
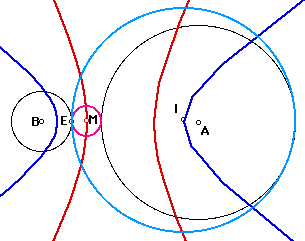
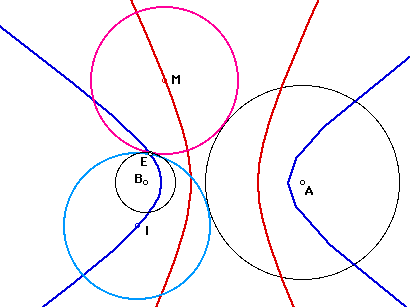
When we are given two circles, we can construct two tangent circles. For example, Given Circle A (black) and Circle B (black), we can construct a tangen circle (I, light blue) and tangent circle (M, pink). When Point E, that is given tangent point, goes on the Circle B, Point I that is the center of blue tangent circle traces BLUE curve and Point M that is the center of pink tangent circle traces RED curve, as follows.
Consider the position of given two circles and the traces, when tangent point E traces on the Circle B. GSP file is here. Script is here.
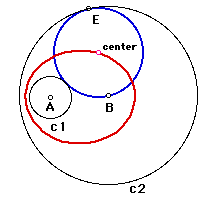
(1) Circle B in Circle A
When E traces on Circle B, the centerI traces ellipse in blue, and the center M traces also ellipse in red, as follows.
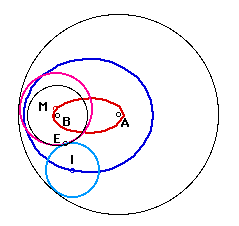
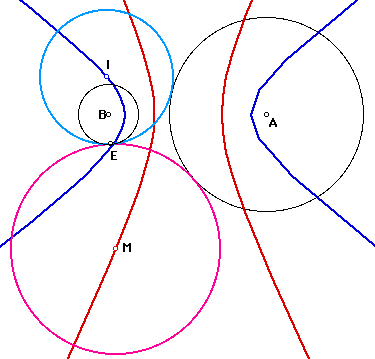
(2)Circle B intersect Circle A
I traces always ellipse in blue. The other side, M traces hyparbola in red, but when E goes on Circle B once, tangent circle M changes line two times. This line is tangent line.
 pink : circle
pink : circle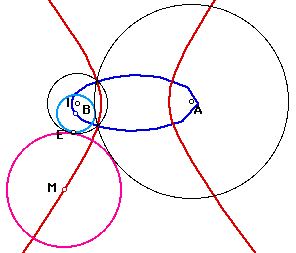 pink : circle
pink : circle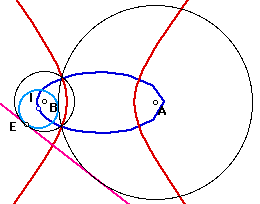 pink : line
pink : line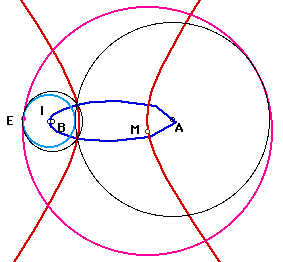 pink : circle
pink : circle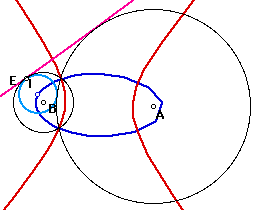 pink : line
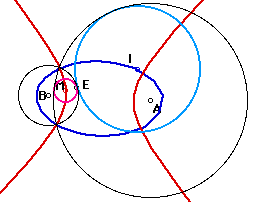
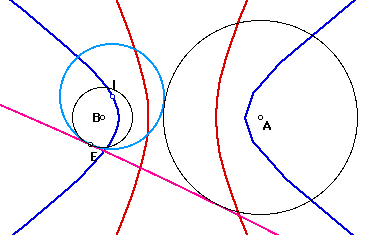
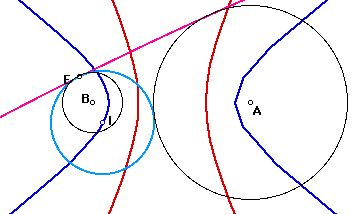
pink : line(3) Circle B leaves CircleA
I and M trace hyparbola. When E goes on Circle B once, both Circle I and Circle M change lines 2times.
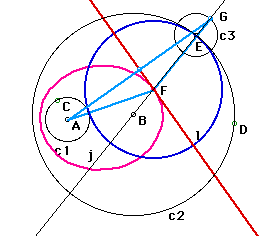
Given A and B. Circle c1 is constructed by center A and point C, and Circle c2 is constructed by center B and point D. Take Point E on the cicle c2 that is tangent point of c1 and c2. Line j connects Point B and Point E. Draw the segment from Point G to Point A, and make Perpendicular bisector l. The 2lines intersect on the Point F. Triangle AFG is isosceles triangle. Gsp file is here.
c1 is in c2
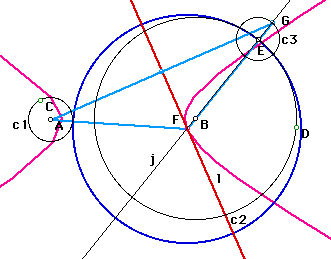
c1 is out of c2
Now consider the redius AC of c1 approach 0, that is, circle c1 approach point A. Consider the locus of F. GSP file is here.
1) Point A is inner c2
Point F trace Ellipse, when E goes around the c2.
(The length of the sum FA + FB is constant, because traiangle
FAE is isosceles triangle, and the radius of BE is constant. Because
BE is the redius of given circle.)
<< Ellipse >>
When FA + FB=constant, Point F traces Ellipse.
This is the definition of Ellipse I learned.
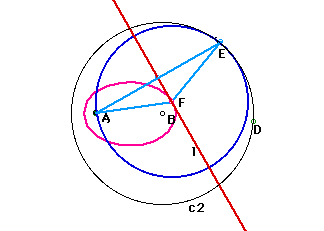
2) Point A is outer c2
when E goes around c2, Intersected point F will trace hyperbora.
(The length of FE is equal to FA, because traiangle FAE is isosceles
triangle.
So the difference of FA-FB=BE is constant, because BE is the redius
of given circle)
<<Hyperbora>>
When FP-F'P=constant, Point P trace Hyperbora.
This is the definition of Hyperbora I learned.