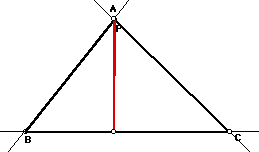
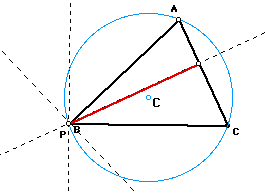
Let triangle ABC be any triangle. Then if P is any point in
the plane, then the triangle formed by constructing perpendiculars
to the sides of
ABC (extended if necessary) locate three points R, S, and T that
are the intersections. Triangle RST is the Pedal Triangle for
Pedal Point P. Here are the sktch
and the script of the Pedal Triangle
for Pedal Point P.
Consider the movemants of the Pedal Triangle.
1. Pedal Triangle
When P is external to the triangle ABC, P is always
consistent with a vertex or external to the pedal triangle. But
when P is internal to the triangle ABC, P is always internal to
the pedal triangle.
When P is moved to a vertex, pedal triangle become a segment, that is on the perpendicular line , from the vertex to the foot of perpendicular of the opposite side.

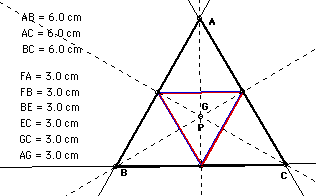
2. Draw the centroid of triangle ABC.
When ABC is regular triangle, and pedal point P is consistent
with the centroid, the pedaltriangle is consistent medial triangle
of ABC.
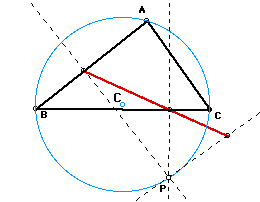
3. Draw the circumcircle and the circumcenter
of triangle ABC.
When P is moved along the circumcircle, three vertices
of the pedal triangle are collinear, that is, pedal triangle become
degenerate. This line segment is called the SIMSON LINE(red line).
When the P is on a vertex, the Simson Line is consistent
with the perpendicular bisector of the opposite side, as follows.
When Pedal point coincidence with circumcenter of the triangle ABC, the vetices of pedial triangle are on the midopoints of the sides of triangle ABC, that is, pedal triangle become mideal triangle of ABC.
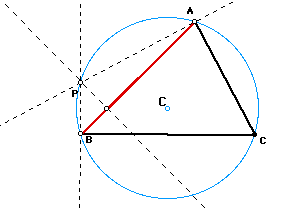
When P is on the intersect point of the perpendicular to AC at the vertex A and the perpendicular to BC at the vertex B along the circumcircle, pedal triangle (on the Simson Line) is consistent with side AB (figure). The same way to the other two points along the circum.circle.
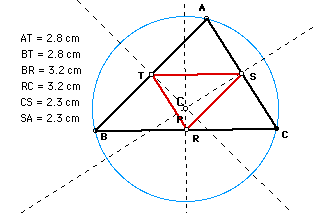
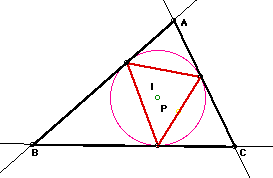
4. Draw the incircle and the incenter of
triangle ABC.
When P is the incenter, the incircle(pink)
of pedal triangle is consistent with the incircle of triangle
ABC.
Put the midpoints of the sides of pedal triangle.
Three midpoints of pedal triangle trace ellipses when pedal point
goes along the incircle, and it seems that the two focuses of
every ellipse are on the the angle bisector(dashed
line of green), as follows.
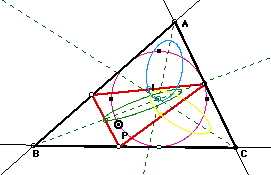
Moreover, the radius of the incircle extend. It seems that the loci of the three midpoints is also ellipse, and the two focuses are on the angle bisectors.
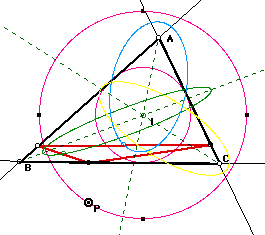
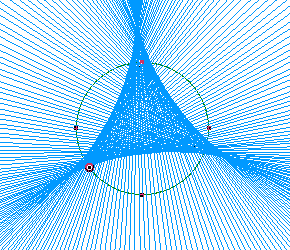
Construct lines on the sides of the Pedal triangle. When the Pedal point goes along the circumcircle of triangle ABC, the Simson Line traces beautiful figure, as follows. It is called a Deltoid. Here is the GSP sketch (with animation).