

Report July,1999 at University of Georgia
THEORY OF THE STUDY
1. Purpose
The purpose of my study is to make the value of using drawing tool software in mathematics classes clear in theory and in practice.
2. Reason for using movement of figures
It is important to enhance the concepts students have about figures as they look at, draw, and work on as many figures as possible. Drawing tool software is helpful for students to understand the shapes and variations of their figures.
For example: Observe the variations of the following parallelograms when sides AD and DC are changed. When students look at the various shapes of the Figure 1, the concept of parallelogram is reinforced.
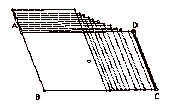
3. How to move the figures (a new way to use the computers)
It is difficult for students to move figures on the notebook, so we use the new tool of the computer. Up to now in Japan, we have used the computers as "the assistant of teaching" for teachers to use in the classroom. For example, using computers, some teachers of computer users wanted to teach in accordance with their aim. They made the program by themselves to solution some specific problem. So students operate computer and learn mathematics in the direction of teachers. We call the way to use the computers like this CAI (Computer Assisted Instruction). That is to say, we think the computer as the tool to manage students to study.
I think I must change how to use the computer. I do consider the computers as "the tool for thinking" and "the learning partner" in the class. I want to use the computer as the tool that students use freely same as a ruler and a compass, and I want to let students use as they like. I use "The Geometer's Sketchpad" as a tool for thinking that is easy for students to use. When we use computer as a new tool, we need to change the way to teach. We need to set up time and space in the class to leave the computers in students' hands, and put emphasis on the activities for students to investigating. I have a good idea that we use the computer network (GSP is equipped with items for network), and in the class we hold in common the marvelous ideas that every student think and discover in common.
4. Evaluation
I let students write impressions and thoughts about the lesson on their notebook at the end of the lesson everyday. They write the impression of the class, the thought that they extend the problem, and the hope that they want to study next lesson, as looking again the class and thinking deeply about the solution of the problem.
I evaluate their aspect of understanding when I read the descriptions of impressions and thoughts of them. I can find in their notebook that the idea of students enhanced gradually.
The reason to evaluate them like this is that I can not understand each process of their study when they study in the classroom. They are absorbed in investigating the problem in the computer, and each student discovers the rules and produce new ideas in each computer.
There are 3 examples that I practiced in my elementary school. I had published example-1 on the Journal of Japan Society for Mathematical Education at Oct.1997.
[Example1] "Let's find the characters of parallelogram!"
DAY:
23/Jan/1996u(A meeting of elementary education to publish the results of our research work in 1996)
STUDENTS:
4grade students (10years old), 38students of my class
PLACE:
Computer Room in Elementary school
(Macintosh LC3, 20machines combined by ether network, 1computer for 2students)
AIM of TEACHING:
The lesson of "Quadrangle"
1.To understand the definitions and the characteristics of the quadrangles (trapezoid, parallelogram, rhombus and so on).
2.To be able to construct the figures of the quadrangles (trapezoid, parallelogram, rhombus and so on).
3.To experience plentifully the fundamental activities about the mutual relationship (parallelogram and rectangle, rhombus and square, and so on) through the activity of drawing the figures of quadrangles.
4.To understand deeply the characteristics of the quadrangles noting diagonal lines of the quadrangles.
The planning on the lesson of "Quadrangle"(11hours)
1st trapezoid.........................................2hours
Definition and construction (1hour)
Characteristics (1hour)---------------using GSP
2nd parallelograms...3hours
Definition and construction (1hour)
Characteristics (2hours)--------------using GSP [this practice1/2]
3rd rhombus............................................2hours
Definition and construction (1hour)
Characteristics (1hour)---------------using GSP
4th diagonal lines................................2hours
Classification of quadrangles by diagonal lines
5th test, looking back........................2hours
Before this lesson, at the lesson of "perpendicularity and parallelism"
Characteristics of rectangle (1hour)------------------using GSP
Characteristics of square (1hour)--------------------using GSP
*Drawing software is "The Geometer's Sketchpad"(Key Curriculum Press, Yano electronics in Japan)
INTENTION OF TEACHING:
Focus on the Discovery of Characteristics of Parallelograms
By last lesson students learned the definition of parallelogram "Parallelogram is the quadrangle has two pairs of parallel sides", and the way to draw parallelogram using triangles combined.
In this lesson, moving the vertices and sides of the parallelogram with GSP they explore the characteristics of the parallelogram. The parallelograms I constructed before the class are in their computer. When they explore, I advise them to note the length of the sides and the angles, and the relationships of the sides and the relationships of the angles. I let them find that what unchangeable are (these are characteristics of the parallelogram) anyhow they move the figure.
When they in all talk about what they explore, they discuss operating the networked computers. On the network, they can send the figures they explored to every monitor of the computer at the same time in a moment, and see the figure of friends move in their presence. So they will hold in common ideas and discoveries, and enhance their concepts of the parallelogram.
WORKS OF TEACHERS BEFORE CLASS:
To explore the figures for students, it is necessary that the figure is able to move keeping its characteristics. So we construct figures according to the definition and characteristics. I prepared a few parallelograms that can move differently.
STUDENTS ACTIVITIES IN THE CLASS:
Moving figures as they like, the students searched the characteristics of figure. They saw the change of values, as measuring lengths of segments, angles, and areas (using "MEASURE" in the menu of GSP). They thought the relation between the change of the shape of figure and the change of values they measured, and found some unchanged relations (i.e.the common characteristics of figure)
DISCOVERIES BY STUDENTS
1) Characteristics of parallelogram
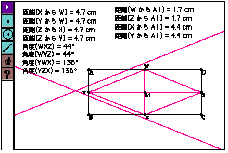
Before exploring AT expected "Angles opposite to each other are equal","Parallelogram will become several quadrangles (square and so on)", and "Diagonal lines cross at the center".

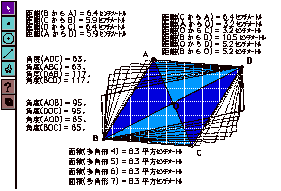
As following figure-2, she measured 4 angles and displayed (ABC, BAD, CDA, BCD), and changed the shape of parallelogram moving vertex A. The values of angles changed variously according to the change of the shape, but she found the equality of angles (ABC=CDA, BAD=BCD). In the same way, She found that diagonal lines cross at the midpoint each other seeing the values of the lengths she measured.
2) Relation of connotation (content of study in middle school)
MJ wrote that moving the parallelogram, the parallelogram sometimes became square and rectangle. She naturally understood the relation of connotation among parallelogram, square and rectangle moving one figure dynamically. She couldn't find if she saw static figures in the text or notebook.
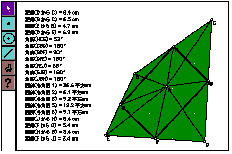
3) Triangles in parallelogram (content of study in middle school)
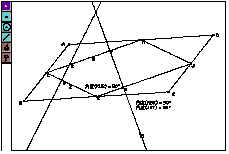
TO created four triangles in the parallelogram by drawing diagonal lines (figure-3), and found equivalence of four areas as measuring each area. After finding, she said 'I want to investigate four triangles next class'.
4) Corresponding angle (content of study in middle school)
KW found corresponding angle at the parallel lines. (figure-4)
5) The sum of interior angles =360degrees(content of study in 5grade)
MH had discovered the sum of interior angles is 360 degrees in the study of trapezoid. She made sure of this on parallelogram. (figure-5) She had been interested in the sum of interior angles through the lesson of quadrangle. She said in her notebook "The sum of interior angles on square, rectangle, rectangle and parallelogram is certainly 360 degree, but one of isosceles triangle and right triangle isn't 360 degree."
I hope students in elementary school to be interested in playing with figures and finding pleasantly many rules and many relations about figures using GSP, and in middle school to prove the rules and relations of figures.
[EXAMPLE 2] What kind of quadrangle do you produce in the quadrangle?
DAY:
23/Jan/1997
STUDENTS:
4grade students (10years old),38students
PLACE:
Computer Room (Macintosh Performa 5220, 20machines, 1 computer for 2 students)
AIM of TEACHING:
The lesson of "Quadrangle"
Same as Example 1.
The planning on the lesson of "Quadrangle"(hours)
1st Trapezoid.........................................2hours
Definition and construction (1hour)
Characteristics (1hour)---------------using GSP
2nd Parallelograms..............................3hours
Definition and construction (1hour)
Characteristics (2hours)--------------using GSP
3rd Rhombus............................................2hours
Definition and construction (1hour)
Characteristics (1hour)---------------using GSP
4th About Quadrangle........................4hours
Quadrangle in the Quadrangle (2hours)--using GSP [this practice1/2]
Classification of quadrangles by diagonal lines (1hour)
Review (1hour)
INTENTION of TEACHING:
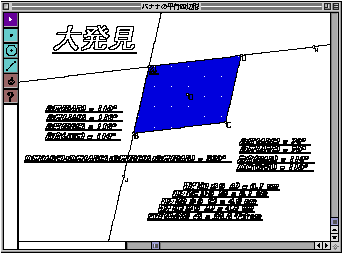
I prepare a quadrangle. Students construct a quadrangle connecting the four midpoints of the sides. They explore what quadrangle constructs when the original quadrangle is general quadrangle? (square?, rectangle?, trapezoid?, parallelogram?, rhombus?) They explore a quadrangle in the quadrangle with GSP by thinking the characteristics of quadrangles that they already learned. On the process of investigation, they enjoy marvelous and fun of the figures, and enhance their concepts of the quadrangle.
About Problem
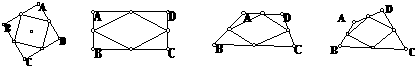
It is interesting for students that a parallelogram is always constructed in the original quadrangle anyhow the original quadrangle is any quadrangle. I think it is important for elementary students to experience to find that quadrangles marvelous, curious, and interesting, and to be surprised at discovery that "a parallelogram is always constructed in the original quadrangle".
It seems that the activities to take a midpoint and construct a quadrangle in the quadrangle are difficult for students, but students who are used to use GSP are able to take a midpoint and to construct a quadrangle, and to draw a diagonal line simply. Actually my student I taught two years ago found "Take Midpoint" from the menu of GSP, and use. (GSP file of student, here)
In respect of improving mathematical thinking, I want students to think generally. When they find one rule, I want them to think any other cases in the process of solution about this problem.
STUDENTS ACTIVITIES IN THE CLASS:
At first, I construct square in the square as a demonstration, and said "What if other quadrangle?"
Many students expected that the same quadrangle may be constructed as the original quadrangle, and they begin to explore. They moved the sides and vertices of quadrangle they want to explore, as noting the lengths of the sides, the angles, and the relations of sides.
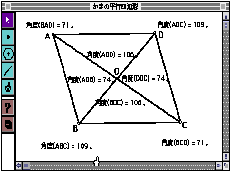
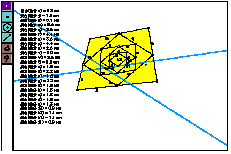
SW thought parallelogram was constructed in the rectangle, and drew two parallel lines (Figure 6) and examined that the two pairs of opposite lines were parallel. Secondly he thought rhombus and measured lengths of four sides, and then he believed firmly rhombus in the rectangle as he find four length is equal.
SA ascertained parallelogram is constructed, measuring the lengths of sides and angles(Figure 7). TN determined that parallelogram is constructed based on the definition of parallelism(Figure 8), and said, "When I draw two perpendicular lines, the angles at the intersection of opposite side are right angle."
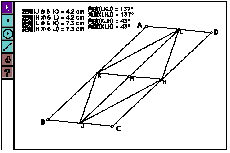
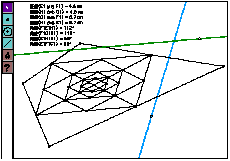
MI found that a general quadrangle generated parallelogram(Figure 9), and said, "I'm surprised. Why parallelogram is constructed?" RY is also pleased with constructing many parallelograms(Figure 10).
At this class, MN explored about parallelogram and rhombus, and wrote on notebook "Today I examined what constructed in quadrangle is. When the figure of friend's send me and they said all quadrangle generate parallelogram, I want to explore ordinary quadrangle next class because I can't believe what they said".
She found at next class that parallelogram are constructed repeatedly in the quadrangle (Figure 11), and wrote" I look at quadrangle in general quadrangle closely. I found the parallelogram is constructed in the parallelogram repeatedly"
HK wrote on his notebook at the end of class "At next class I want to investigate isosceles triangle and regular triangle." Then at the next class he investigate triangles and found constructed triangle is same shape as the original triangle and the area of constructed triangle is equal to the area of original triangle (Figure 12, Figure 13).
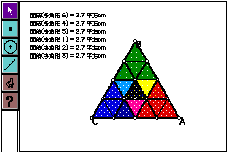
[EXAMPLE 3] Let's make the moving pictures (Symmetrical Figures)!
DAY:
23/Jan/1999 (photo)
STUDENTS:
6grade students (12 years old), 38students
They are always able to use computers at rest time and after school. They use Kidpics (drawing software for kids), Clarisworks, Eudra (mail software), www-browse software at computer time, and they use GSP at mathematics class for 5hours by this class.
PLACE:
Computer Room (Macintosh Performa 5220/20machines combined by ether network,u1computer for 2students)
AIM of TEACHING:
The lesson of "Symmetrical Figures"
1. To reinvestigate fundamental plane figures from a point of view of line symmetry and point symmetry, and to be interested in the beauty of figures, and to investigate figures enthusiastically.
2. To enhance the conceptions of plane figures operating figures.
3. To be able to construct line symmetrical figures and point symmetrical figures based on the definition and the characteristics of figures.
4. To understand what line symmetrical figures and point symmetrical figures are.
The planning on the lesson of "Symmetrical Figures"(12hours)
1st line symmetrical figures.....................4hours-----using GSP
Characteristics of line symmetrical figures
Construction of line symmetrical figures
2nd point symmetrical figures...................3hours-----using GSP
Characteristics of point symmetrical figures
Construction of point symmetrical figures
3rd polygon and symmetry............................2hours
Symmetry of Regular polygon and circle
4th Review...........................................................3hours
Construct moving figures! --------Using GSP [this practice 2nd/3]
INTENTION of TEACHING:
The purpose of this class is to move symmetrical figures students construct and to enjoy symmetrical movements and changes of figures.
At first they produce figures and pictures symmetrically using triangles, quadrangles and circles. And using animation they move the piece symmetrically. Looking pieces each other, they discuss the movements of symmetrical figures.
STUDENTS ACTIVITIES IN THE CLASS:(some pictures : )
Strawberry Group:
Students drew half of the face of friend, and established an axial of symmetry. They completed the picture using the symmetric transformation of the menu. Then they created animation, that is one of a function of moving figures automatically, and enjoyed moving the figure with animation (Figure 14).

KK (Strawberry Group):"It is pleasant for me to construct various figures, and move symmetric figures. I enjoyed constructing line symmetry and point symmetry in the figure ". Secondly they the make a problem to friends "where is used symmetry in the figure?, as hiding the axis of symmetry and the point of symmetry (Figure 15).
Persimmon Group:
They made a picture of pinwheel with point symmetry, and moved a vertex on a circle (Figure 16). They completed beautifully beyond expectation, explained "We made the point symmetric figure with animation, the point of symmetry is at the coincident point of four vertices of triangles.

DISCOVERIES BY STUDENTS
1) Symmetric figures mutually (using symmetric transformation)
At the lesson of symmetrical Figures students in elementary school in Japan study the plane figures of symmetrically itself like as rectangle, parallelogram and isosceles triangle. The other side, symmetric figures mutually are learned in secondly school.
Students of Turtle Group found the way to transform figures symmetrically in the class when they exercised to make quadrangle combining two triangles (Figure18).

After finding symmetric figures mutually, they drew figures using symmetric transformation (Figure 19). At first, they construct a figure above left, and transformed symmetrically at the tangent point of circles, moreover they transformed again establishing the axis of symmetry. When they moved a point of figure (above left,) the points and sides located symmetrically are moved at the same time, so they enjoyed movements of four figures.
2)Curious movement of figures
A girl of Apple Group moved isosceles triangle with animation, she was pleased with a curious movement of triangle, as follows. All students enjoy this animation. She moved vertex B along a circle and vertex C along a segment.

3) Move an axis of symmetry
Students enhanced the concepts of line symmetry and point symmetry when they constructed the figures and saw to move the figures symmetrically. They enjoy making funny movements and seeing the beauty of symmetry.
The purpose of the class was to reinvestigate fundamental plane figures from a point of view of line symmetry and point symmetry. I think students understood deeply the figures like triangles and quadrangles, through the activity of learning dynamic symmetrical figures, and they will see figures and shapes around them in their life from a viewpoint of symmetry.
*Here are some sckeches students produced.
4 people | Angel | Butterfly | Cat | Face | Ladybird | Mt.Fuji | Pierrot | Rabbit | Snowman
Finally
I think it is difficult in Japan for anyone to understand the world of technologies like GSP and Graphic Cariculater, because only people who actually experience the fun of dynamic feeling of technology realize the value of using technology in mathematics education. Secondly we cannot express in papers how change the dynamic figures and graphs. So I am going to show teachers in Japan many classes using technology as possible, and make the value of using technology spread.
-----------------------------------------------------------------------------------------------------------------
Thank you for reading my report.
Would you like to send e-mail to me after reading the above report of mine?
I will refer to your suggestion and helpful, instructive opinion, and I am going to make an effort from now on to improve mathematics education in Japan.
--
office/
Elementary School attached to University of Yamanashi
1-4-1 Kitashin Kofu, JAPAN zip400-0005
Tel:*81-55-220-8291/Fax:*81-55-220-8785
home/
7-10-22 Kokubo Kofu, JAPAN zip400-0043
Tel:*81-55-226-1599