

PROBLEM: Average Rate
Danielsville is 20 miles frm Jim's home in Athens. He Drives
60 mph going to a meeting (he is almost late) but coming home
the weather is bad and drives 30
mph. What is his average speed for the time he is on the road?
A. Discuss why 45 mph is not correct.
Going to D'ville took 1/3 of an hour. Coming home took 2/3 of an hour. So the total 40 miles took one hour. The speed is 40 mph.
B. Use
d = r t
to verify and develop an understanding of how to find average rates. Elaboration.
In the following problem, rate is represented by a (where a = rate 1) and b (where b = rate 2); and time is represented by x (where x = time 1) and y (where y = time 2).
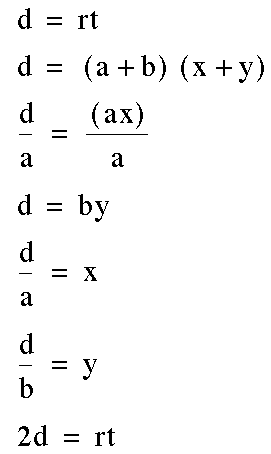
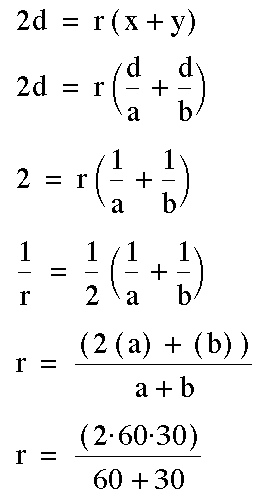
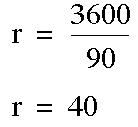
If you look at the amount of time spent on the road going and coming, then the average rate is easily calculated. The reason we did not simply use the speeds is because time was a factor that entered into the picture. If no other information was given or factored into the formula then the 45 mile per hour rate would be reasonable and applicable.