

Exploration
Construct any triangle. Construct an angle bisector in the
triangle and draw the segment along the angle bisector
from the vertex to the intersection with the opposite side.
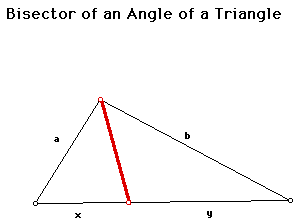
Measure the ratio of the adjacent sides. In the triangle pictured here we have:
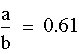
Measure the ratio of the segments cut off by the bisector on the opposite side. In the triangle pictured here we have
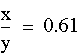
Repeat for many triangles. Click here for a GSP Sketch to explore these ratios.
TO PROVE
The bisector of an angle of a triangle divides the opposite side into segments that are proportional to the adjacent sides.
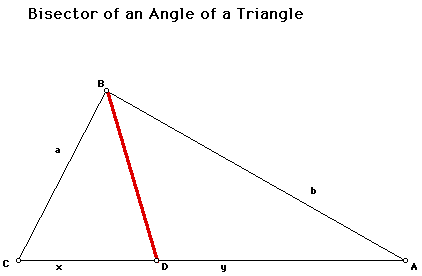
That is, for any triangle ABC, the bisector of the angle at C divides the opposite side into segments of length x and y such that
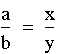
In triangle ABC, segment BD is the angle bisector of the triangle, creating angles that are of equal degree measure, i.e. <CBD = <ABD.
To corrected:
If two angles are congruent, then we know that the sides opposite those angles are congruent. So, we know that segment x is congruent to segment y, because angles CBD and ABD are congruent due to the bisection of angle B with an angle bisector.
What we were trying to prove is that if the triangles are similar, then their sides are proportional. Two triangles are similar if the angle of one triangle is congruent to the angle of the other triangle and the sides including these angles are in proportion.
Now we conclude that C= C, and A = A, and therefore the ray that bisects its angle will create two congruent angles (that is, they are of equal measure) and it will bisect the the side opposite its angle, but the angles formed at this side will not be right angles nor congruent angles, however, the sides created (x and y) will be in direct proportion to one another, as will the sides a and b.
Can you add your findings to this investigation or will you create a totally new investigation that will not show the same data? Make conjectures and send me an e-mail.