

A man named Khari writes a check for d dollars and c cents. The clerk gave him c dollars and d cents, by error, and after spending 5 cents, Khari finds the remaining money is twice the amount of the check. Determine the amounts.
This question needs to be stated to
the class: Okay, you
have a start, can you complete this to make sense of it? What
other information do I need to know? Is this problem really relevant
to me? Can this type of situation really happen to me? If it ever
does, what steps would I take to remedy the situation? What now?
A) Can we make a table? a chart? a picture? act it out?
Should we look for any distinct patterns now? or should we conduct some sort of search for the answer? Should we guess and check? (Kids must have some sort of starting point in order to get the effects of the "life lessons" that we are trying to teach them. I can say that there are times when kids do not need any help getting started and finishing up their tasks...but those times are not ALWAYS. For those students who struggle at all lessons of mathematics, they will need those extra boosts, those extra incentives, those extra pats on the backs...it may be the only time they are being encouraged).
B) Let's make a table. Then let's look for some sort of pattern.
|
|
199d + 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Is there some sort of pattern that is going on within this table? What could it be? Should the table be extended to include more data? Is this enough data?
If you notice, the numbers in red represent the numbers I originally started with. I did not or could not see a pattern within this arrangement of a table, so instead I added the black numberals to represent the numbers I added in to try and complete my table.
By extending my table, I found that there was a pattern between the difference of 199d +5 and 98c. The pattern showed that there was an increase in the number from/to each level by 3. For example, when d = 9, the difference between the the two equations was 32, and when d = 10, the difference between the two equations was 35...therefore, a difference of 3 = 35 - 32.
Other than this overt cue in the differences, I found nothing else that really said to me..."Okay, now you need to start on this step."
C) Let's solve the given equation.
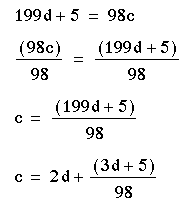
D) Okay, what is the answer already???
By extending the table a little more and only having included the odd numbers...see, the man already spent 5 cents, so I believe this has a big bearing on what the table could or should look like...we get to the following portion of the equation within the table:
|
|
|
|
|
|
|
|
|
|
|
|
See, the differences up until this point constantly remained 3. The two equations became equal at d = 31 and c = 63, with a difference of 0!!!