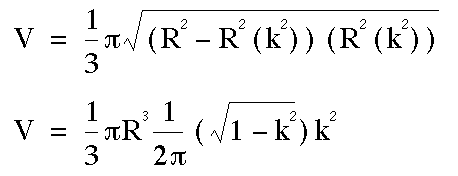Problem: Maximum Volume of a Cone
A circular disc of radius R is used to make a Cone by removing a sector with angle ø and then joining the edges where the sector was removed. What is the maximum volume that such a cone can attain? That is, what angle ø for a disc of radius R would you remove to make a cone of maximum volume?
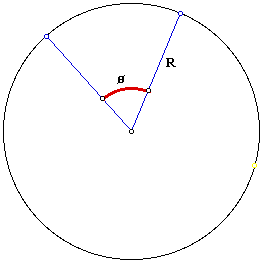
In this illustration the sector of the circular disc is removed and the edges joined to form the cone as shown below where r is the radius of the base of the cone. The circumference of the base of the cone is: 2 * pi *R - theta * R.
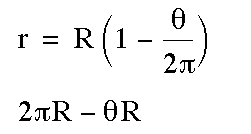

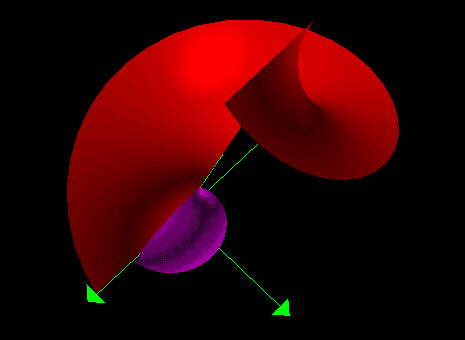
The three figures above do not look like my cone at all, so we must find an alternative way to show the problem:
I have been trying to create the cone but, I have failed to do so...maybe a bit more practice and I will be there!
Let's turn our attention back to the problem at hand...what do we do next? Take a look at the hint Dr. Wilson gave by clicking here!
Let's start out with some fundamental things that we already know:
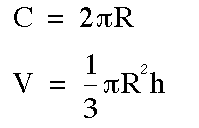
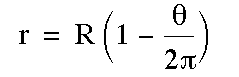 .
.Now we let 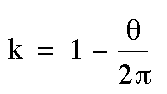 . Then r = kR and
the height of the cone h will be
. Then r = kR and
the height of the cone h will be 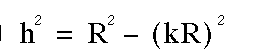 or
or ![]() .
.
Let's keep in mind that a sector or part of the disc was removed,
so what did we have left? or better yet, what do we call that
missing part? Right now we will call the missing part k. So my
sector of the disc would equal: 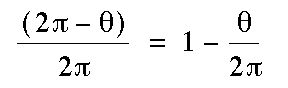 .The
"what do we have left" would be:
.The
"what do we have left" would be: ![]() .
And remember that the volume of the cone is
.
And remember that the volume of the cone is 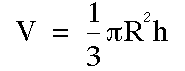 .
.
The volume of the cone becomes
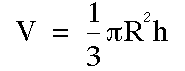
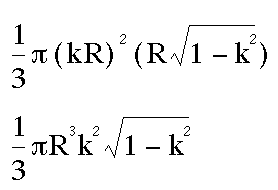
Now 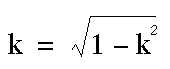 or
or 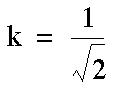
The radius of the circular base of the cone is: 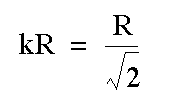
and the height becomes: 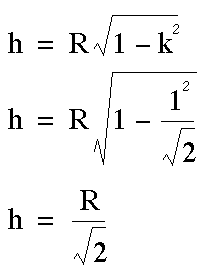
So now we are faced with the what the maximum volume of the cone is or becomes: