Problem: Rational or Irrational

To see a detail statement of the problem, click here.

Let and assume that x is rational, however it is not an integer. There should exist a minimal positive integer n such that xn is an integer. Consider . Since the fractional part of x,

Note that mis an integer for m=nx-n[x] which is an integer. Also, 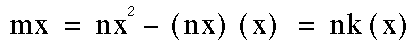which is also an integer. Due to the minimality of n, m=0. In other words, x =[x] and is an integer in contradiction to our assumption.

Reference:

http://cut-the-knot.com/content.html