Prove that the Square Root of 2 is an irrational number.

Discussion: That is, prove that this number can not be expressed as a rational
fraction in lowest terms,

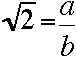
where the greatest common divisor of a and b is 1.

For what positive integers N does your proof generalize to show that

is irrational?

Why? or Why not?

Show irrational.

First, let us look at some simpler square roots:

1) or

2) or

Now notice that the answer to and the answer to . Between 1 and 2 there is not a square root whose answers could or would be an integer, maybe not even a rational number.

What about finding a rational number in the form of , where its square root equals 2? We assumed that if is rational, then

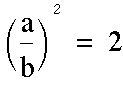
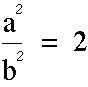
Because of this equation: then the Fundamental Theorem of Arithmetic says that the prime factorization is .

Because , no matter how many times that 2 appears within the prime factorization of one b, then it will only be twice as many in or . There's also an odd number of twos in this problem and it cannot appear as an odd number and an even number within the same prime factorization, and so there is a contradiction here.

Here are more of our reasoning:

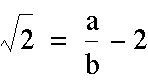
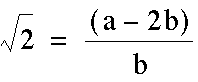
the frac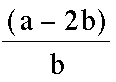tionproduces a rational number. Can you explain why the above equation is not rational? Can you explain why the fraction 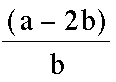is a rational number?

Want another way to look at this problem? Alright, let's look!

Suppose we have a rational number 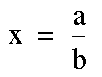with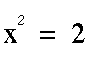

We assume a and b are relative prime, then, 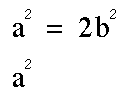is even, so a is even and a = 2k.

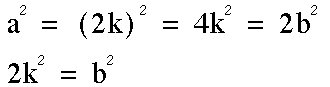
So b is also even.

We stated that a and b are relative primes and a contradicts for an integer a = b such that am + bm = 1.

Reference:

Billstein, R., Libeskind, S., & Lott, J.W. 1993. A Problem Solving Approach to MATHEMATICS for Elementary School Teachers (fifth edition). Addison-Wesley Publishing Company, Inc.

Return