for

Shanti Howard

Assignment 1 Problem #6: Graph the following equations:

x^2 + y^2 = 1

x^3 + y^3 = 1

x^4 + y^4 = 1

x^5 + y^5 =1

In the following assignment, I will show, through the use of Graphing Calculator, that 1) as the exponents of the above functions increase, there will be a significant change in their output or graph, 2) there will be major difference between the graphs of even functions to odd functions, and 3) when the function is set equal to z....well, you may find this one out on your own. Follow me so that you may journey through the land of functions. Have a marvelous time!

 

 

 

 

Figure 1

 

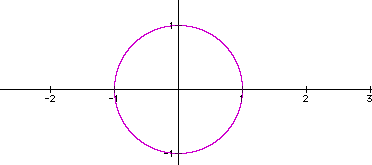
The graph of x^2 + y^2 =1. As you can very well see, the graph of x^2 + y^2 = 1 makes a complete circle with a radius of one unit.

 

 

Figure 2

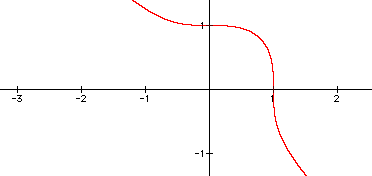
The graph of x^3 +y^3 = 1. Notice how the graph above differs from this one. I wonder if the graph of x^4 + y^4 will be different than the two pictured here. The curve of this graph suggests that it wanted to make some sort of revolution, but as my middle schoolers would say "it got off track."

 

 

Figure 3

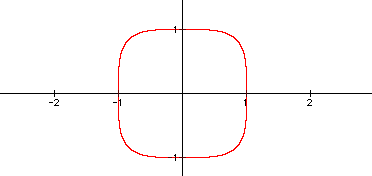
The graph of x^4 + y^4 = 1. See the difference between the the cubed function and the fourth function. Can you see the likeness of Figure 1 and Figure 3? I wonder if the graphs of even numbered powers will be similar and the graphs of odd numbered powers will be similar. I guess, I need to probe deeper to find that answer.

 

Figure 4

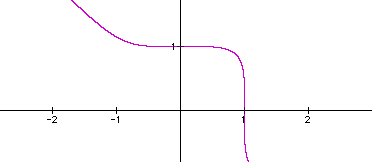
The graph of x^5 + y^5 = 1. It looks as if Figure 4 is approaching the image of a half square. It does look a lot like Figure 2. My hypothesis is that as even numbered exponents get larger, the coordinates of the "verties" reaches (1,1), (-1,1), (-1,-1), and (1,-1). This image will perhaps become a square. As odd numbered exponents get larger, their image becomes a quarter square in the first quadrant and its endpoints seem to go off indefinitely in the second and fourth quadrants. Let's look at a few more images:

Figure 5

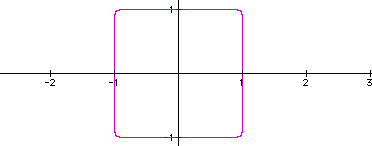
The graph of x^24 + y^24 = 1. Most certainly looks as if it is reaching its limits of being a square.

 

Figure 6

The graph of x^25 + y^25 =1. I would say that if I were to lay this image on top of Figure 5, it would almost be a perfect fit...that is, in the first quadrant. Let's turn our attention to our last two functions. What do you think will happen if the exponents get larger than 24 or 25? Take out a scratch sheet of paper and draw your hypothesis!

Do you want to find out? Let's see below:

 

 

 

 

 

Figure 7

Figure 8

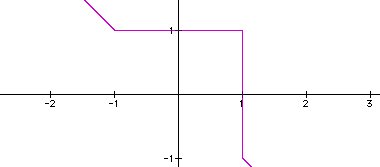
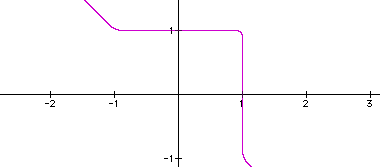
Can you guess the functions of the two graphs pictured in Figures 7 and 8?

 

Figure 9

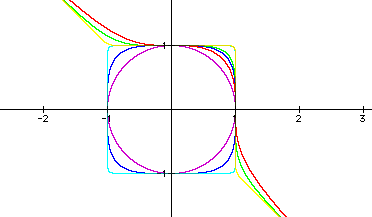
The above graph depicts all the graphs as they would appear together.

 

Okay, I told you that we would look at an equation(s), one like those above, that was set equal to z.

Figure 10

The graph of x^10 + y^10 = z. Can you see how the graphs of two dimensions and three dimensions vary. You can see the depth of this image!

 

Figure 11

 

 

Return