for

Shanti Howard

Assignment 10

Parametric Curves

 

A parametric curve in the plane is a pair of functions

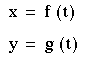
where the two continuous functions define ordered pairs (x,y). The two equations are usually called the parametric equations of a curve. The extent of the curve will depend on the range of t and your work with parametric equations should pay close attention the range of t . In many applications, we think of x and y "varying with time t " or the angle of rotation that some line makes from an initial location.

Various graphing technology, such as the TI-81, TI-82, TI-83, TI-85, TI-86, TI-89, TI- 92, Ohio State Grapher, xFunction, Theorist, Graphing Calculator 2.1, and Derive, can be readily used with parametric equations. Try Graphing Calculator 2.2 or xFunction for what is probably the friendliest software.

EXPLORATIONS

Graph

x = cos(t)

y = sin(t)

 

Look at the following figures below. Look for some sort of pattern that would distinguish one from the other, other than the obvious.

Why did I choose for the starting point of this investigation? Why did the parameters for each successive figure decrease at the rate they did?

 

Examine Figures 1 and 2.

Figure 1:

 

 

 

Figure 2:

 

Now, compare the previous two figures with Figures 3 and 4. What do you notice?

Figure 3

Figure 4

 

What can be said for Figure 5? Compare and contrast the above figures with Figure 5.

Figure 5

 

 

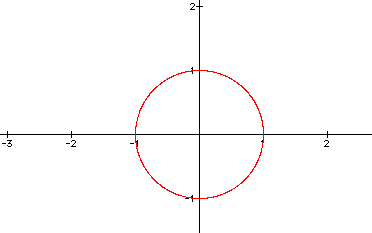
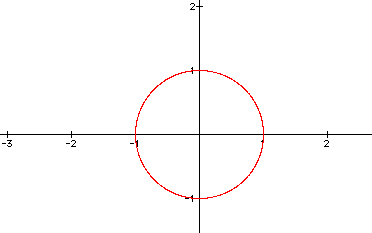
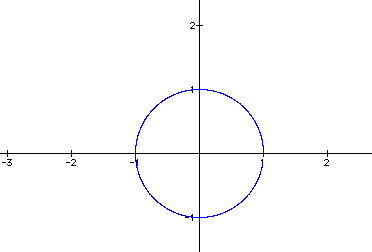
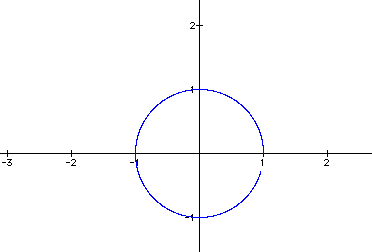
How would you change the equations to explore other graphs? Did this investigation prove to be a boring investigation as Dr. Wilson put it?:o)

 

 

 

 

 

Graph

 

Figure 1

A replication from Graphing Calculator 2.2

What might its parameters consist of ?

Figure 2

Figure 3

Figure 4

Figure 5

 

 

Figure 6

Figure 7

Figure 8

Click excel worksheet on the parameters of the x and y coordinates.

 

 

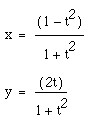
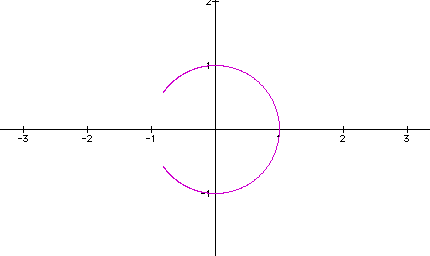
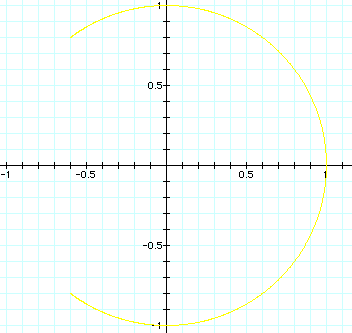
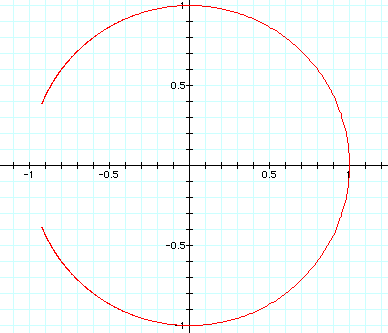
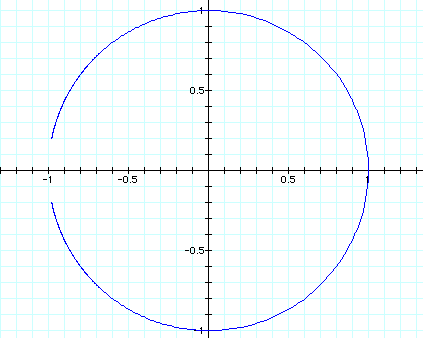
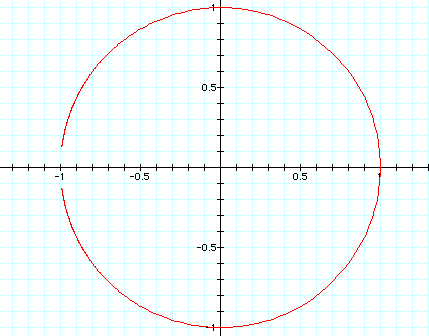
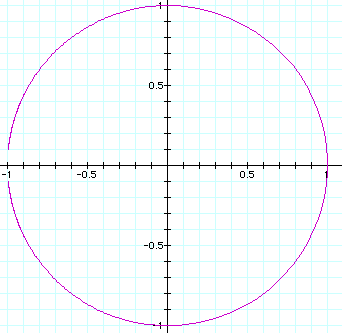
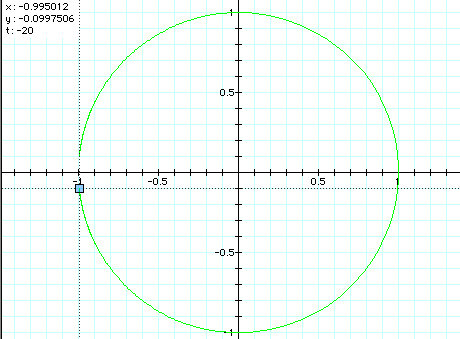
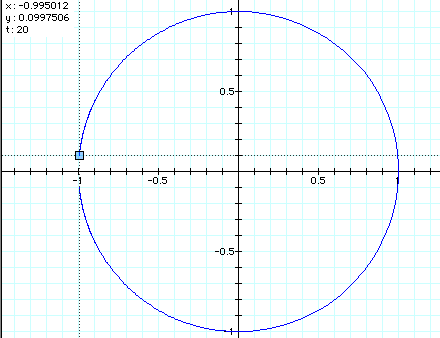
Interpret. What would you change to explore and understand the graphs?

I did not get, let alone understand, parametric equations before entering its domain. I still do not think I get parametric equations as I had hoped I should. Maybe a little time and hope and lots of patience will at least get my foot stuck in its door.

On all of the graphs, the parameters are getting close to the value of -1, thus trying very hard to create a complete circle. But if you look closely at the firgures above it never does. I even tried to go beyond the parameters of -20 and 20, but as the numbers increased, the figure itself began warping and thus the creation's pixels made it all wrong! I could not understand why and neither could Dr. Wilson. Therefore, he came to the solution that something was off with the pixels in Graphing Calculator 2.2.

If you examine my excel document, it shows that the parameters almost get close to making a complete circle, but it fails to do so.

Return