

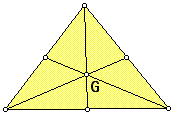
1) The CENTROID (G) of a triangle is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side.
Use Geometer's Sketchpad (GSP) to Construct the centroid and explore its location for various shapes of triangles.
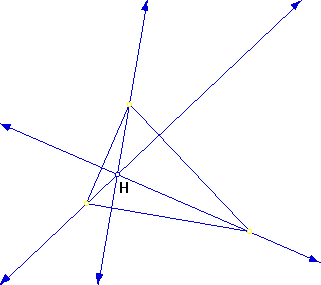
2) The ORTHOCENTER (H) of a triangle is the common intersection of the three lines containing the altitudes. An altitude is a perpendicular segment from a vertex to the line of the opposite side. (Note: the foot of the perpendicular may be on the extension of the side of the triangle.) It should be clear that H does not have to be on the segments that are the altitudes. Rather, H lies on the lines extended along the altitudes.
Use GSP to construct an orthocenter H and explore its location for various shapes of triangles. (Make sure your construction holds for obtuse triangles.)
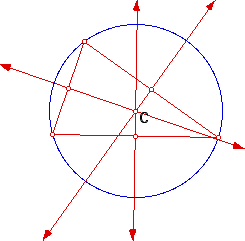
3) The CIRCUMCENTER (C) of a triangle is the point in the plane
equidistant from the three vertices of the triangle. Since a point
equidistant from two points lies on the perpendicular bisector
of the segment determined by the two points, C is on the perpendicular
bisector of each side of the triangle.
Note: C may be outside of the triangle.
Construct the circumcenter C and explore its location for various shapes of triangles. It is the center of the CIRCUMCIRCLE (the circumscribed circle) of the triangle.
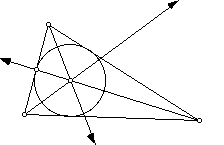
4) The INCENTER (I) of a triangle is the point on the interior of the triangle that is equidistant from the three sides. Since a point interior to an angle that is equidistant from the two sides of the angle lies on the angle bisector, then I must be on the angle bisector of each angle of the triangle.
Use GSP to find a construction of the incenter I and explore its locationfor various shapes of triangles. The incenter is the center of the INCIRCLE (the inscribed circle) of the triangle.
5) Use GSP to construct G, H, C, and I for the same triangle. What relationships can you find among G, H, C, and I or subsets of them? Explore for many shapes of triangles.
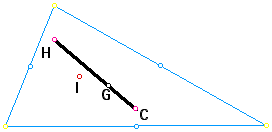
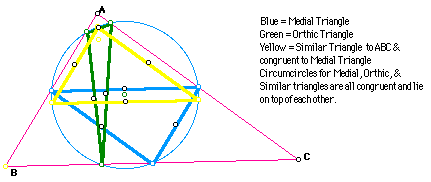
6) Take any triangle. Construct a triangle connecting the three midpoints of the sides. This is called the MEDIAL triangle. It is similar to the original triangle and one-fourth of its area. Construct G, H, C, and I for this new triangle. Compare to G, H, C, and I in the original triangle.
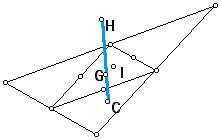
7) Take any acute triangle. Construct a triangle connecting the feet of the altitudes. This is called the ORTHIC triangle. Construct G, H, C, and I for the orthic triangle. Compare to G, H, C, and I in the original triangle. Can you extend this to right triangles or obtuse triangles?
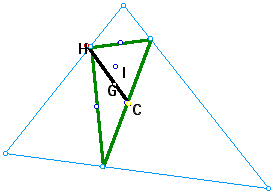
8) Take an acute triangle ABC. Construct H and the segments HA, HB, and HC. Construct the midpoints of HA, HB, and HC. Connect the midpoints to form a triangle. Prove that this triangle is similar to triangle ABC and congruent to the medial triangle. Construct G, H, C, and I for this triangle. Compare.
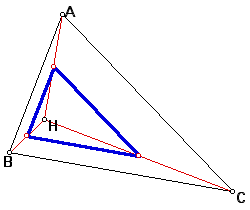
9) In the same original triangle, construct the three secondary triangles of Exercises 6, 7, and 8. Construct the circumcircle for each of the secondary triangles. What do you observe? Can you prove your conjecture?
10) The Nine-Point circle for any triangle passes through the three mid-points of the sides, the three feet of the altitudes, and the three mid-points of the segments from the respective vertices to orthocenter. Construct the nine points, locate the center (N) and construct the nine point circle.
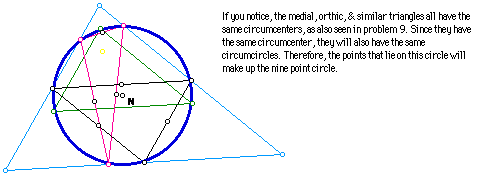
11) How is N related to G, H, C, or I for different shaped triangles?
It seems as though when the points of the large (original) triangle moved to make a new triangle, N stayed along the same line (or even in the same plane) as G, H, C, and I. However, when the triangle became an obtuse triangle N, G, H, C, and I were no longer seen. When the triangle was a right triangle, the points overlapped.
Write-Up
The exploration of finding the centers of a triangle has proven to be a worthwhile activity for my upcoming sixth grade mathematicians! Although I would not introduce the terms centroid, orthocenter, circumcenter, incenter, etc. as they are beginning the activities with this discovery, I would allow my kids to "explore" the world of Geometer's Sketch Pad. I would rally them on to make up terms on their own. Once they have completed their studies of the centers of a triangle, I would then kindly introduce all the terms they have been playing with and then ask how their terms are similar and or different than the ones I have actually given.
The plan:
Place students in groups of three.
Assign jobs: artist, transcriber, and public relations
Artist: In charge of all designs of upcoming triangles
Transcriber: In charge of all note-taking, making sure to have step by step details of each and every drawing.
Public Relations: In charge of all public speaking of and about the the relationships of points on and in triangles and circles that may be related to the given triangle.
Each group will be given two to three different "discoveries" to interact with. The students must: 1) construct triangles (and circles) using a compass and a straight edge, 2) name the triangles and the constructed circles, 3) make up terms to describe the activities they are involved in (this information will be withheld until the completion of the activity), 4) write down all steps that were involved in the process of making their creations, 5) relate the step by step process to the class for notes, 6) question all that is and all that may or may not be, 7) students must interact with one another on this activity, 8) if there is a student(s) who wish to work alone, only give two discoveries and allow the student to present his or her findings.
Once activities are completed, the students will once again form groups...different ones this time and answer the following questions. If need be, the same job titles can be assigned or chosen if the groups would like this.
The groups will share their ideas about the questions below, and present their ideas once the entire class reconvenes. If needed, I will also ask for volunteers to show the class the "how to's" of this activity.
The questions follow below:
1) Prove that the three perpendicular bisectors of the sides of a triangle are concurrent.
2) Prove that the lines of the three altitudes of a triangle are concurrent.
3) Prove that the three medians of a triangle are concurrent and that the point of concurrence, the centroid, is two-thirds the distance from each vertex to the opposite side.
How would you use GSP to help students understand this relationship of the triangle and its medians? How would you develop a sense of proof of the relationship with students?
4) Prove that the three angle bisectors of the internal angles of a triangle are concurrent.
5) Prove that any angle bisector of a triangle is concurrent with the two angle bisectors of the opposite exterior angles of a triangle.
6) Take a point of concurrence as determined in Problem 16 and construct a circle tangent to the lines of the three sides (of the triangle)
7) Prove that for any triangle, H, G, and C are collinear, and prove that HG = 2GC.