

Assignment 6, Problem #1
Construct a triangle and its medians. Construct a second triangle with the three sides having the lengths of the three medians from your first triangle. Find some relationship between the two triangles. (E.g., are they congruent? similar? have same area? same perimeter? ratio of areas? ratio or perimeters?) Prove whatever you find.
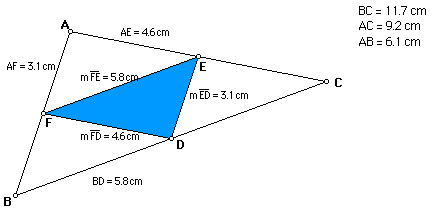
Go to Text for Figure 1
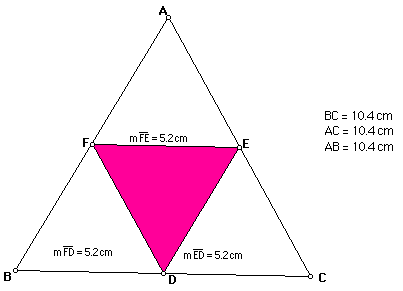
Go to Text for Figure 2

Go to Text for Figure 3
In Figure 1, triangle ABC was constructed using three arbitrary points. Once the triangles were constructed, the midpoints or medians were also constructed. I decided to connect the three medians to make a second triangle to see if the this new triangle was going to have the lengths of the three medians from my first triangle. They did!! I do not know why, but I never really realized this...maybe I need to have more investigative studies for my students so that they may have beautiful discoveries such as this simple one!
In Figure 2, the equilateral triangle ABC is given with its correlating sides. If you notice, the sides of triangle FED are the lengths of the medians of triangle ABC. Also, triangle FED is similar, not congruent, to triangle ABC. It is similar to triangle because the segments in ABC are twice the length of the segments in triangle FED.
In Figure 3, notice that the perimeter of triangle ABC is twice that of triangle FED. Also look at the areas of both triangles. What do you notice here? What can you say about the ratios of the larger triangle to the smaller triangle? Could you create another triangle, say an obtuse triangle and the outcomes remain the same? Can you make a conjecture about your findings?