for

Shanti L. Howard

1. Construct any triangle ABC.

 

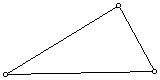
2. Construct the Orthocenter H of triangle ABC.

 

 

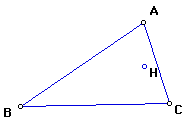
3. Construct the Orthocenter of triangle HBC.

 

 

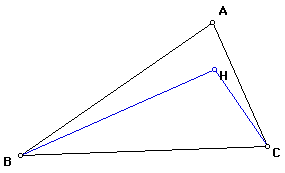
4. Construct the Orthocenter of triangle HAB.

 

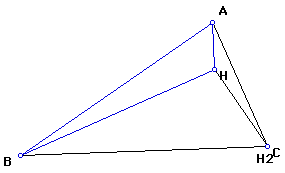
5. Construct the Orthocenter of triangle HAC.

 

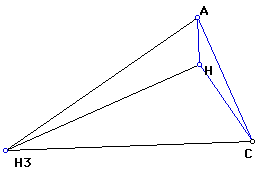
6. Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC.

Circumcircle of triangle ABC:

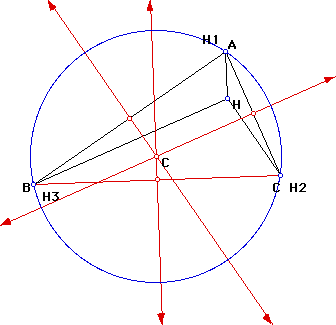
Circumcircle of triangle HBC:

 

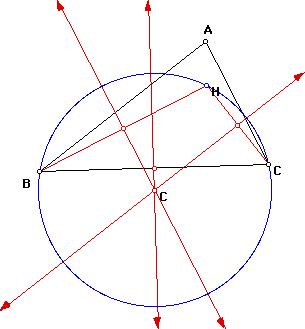
Circumcircle of triangle HAB:

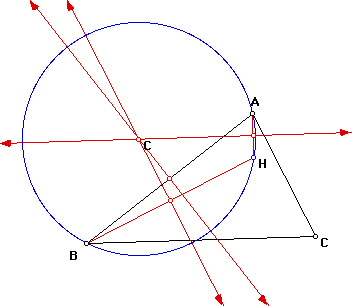
Circumcircle of triangle HAC:

 

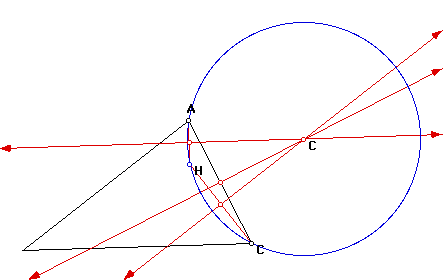
7. Conjectures? Proof?

I could not find anything that really jumped out at me when I did the orthocenters and circumcircles of these triangles. I can conjecture though that triangles that are named are always within the the circumcircle, hence the name...circumcircle. I also noticed that by scrolling from one circle to the next, I found that as the circumcircle was made on triangle ABC, segment BC was highlighted in RED. When I observed the circumcircle of triangle HBC, I found that segments HB and HC were highlighted in RED. This same condition was also true for triangle HAB, where segments HA and HB were highlighted in RED; also for triangle HAC, where segments HA and HC were highlighted in RED. What does this say for the constructions or the circumcircles or even the orthocenters. I do not know the answer to this one. Maybe you can e-mail me with some information about it. It would certainly be helpful to my students...and of course their loving teacher!!! If you continue on, I do believe I have stumbled onto something quite interesting!!!

 

 

8. Construct the nine point circles for triangles ABC, HBC, HAC, and HAB.

Nine Point Circle for triangle ABC:

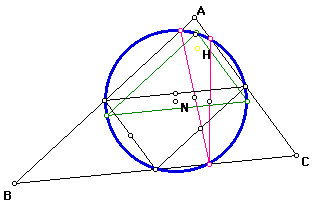
Nine Point Circle for triangle HBC:

Figure 1

Figure 2

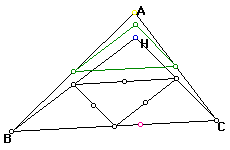
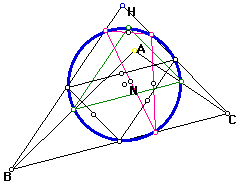
Nine Point Circle for triangle HAC:

Figure 1

Fiure 2

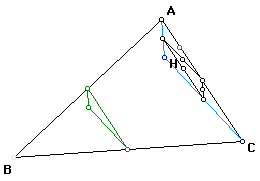
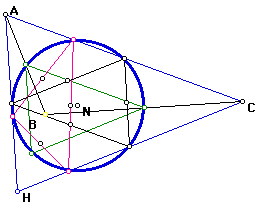
Nine Point Circle for triangle HAB:

Figure 1

Figure 2

 

 

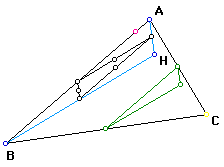
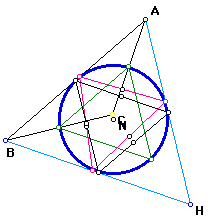
9. Construct triangle ABC, its incircle, its three excircles, and its nine-point circle. Conjecture?

Look at the dashed lines in each figure below. What do you see in each figure? Are there any major changes from one phase to the next? Also, look at each shape of the triangle being presented. What shapes are there? What sort of conjecture can you come up with about the triangles and the figures made by the dashed lines? How were the figures made? Hint: Construct problems 1-6, 8, &9. You may do this now by clicking:

here for the script of an orthocenter (don't forget to choose 3 points first and follow the directions above)!

here for the script of circumcircles

here for the script of the nine point circles

here for the script of the incircle

here for the script of an excircle

Figure 1

Notice that triangle ABC is an equilateral triangle.

 

 

Figure 2

Now notice that triangle ABC is an isosceles triangle.

 

Figure 3

Can you guess what type of triangle triangle ABC is NOW?

 

Figure 4

Triangle ABC is now a scalene obtuse triangle. Notice the differences among the triangles.

 

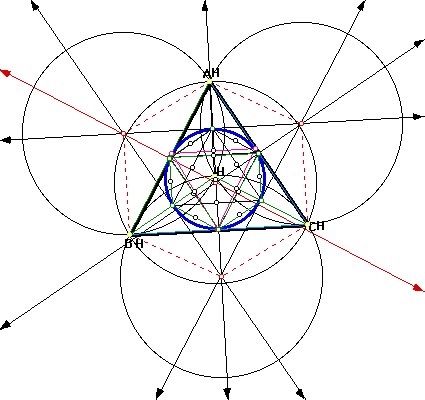
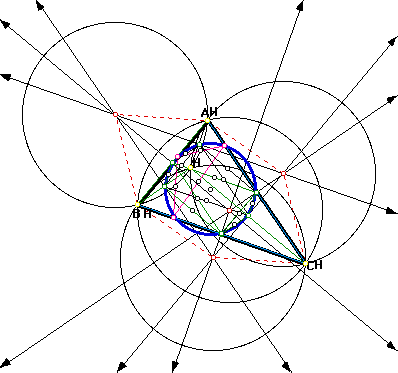
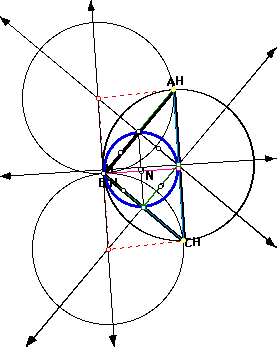
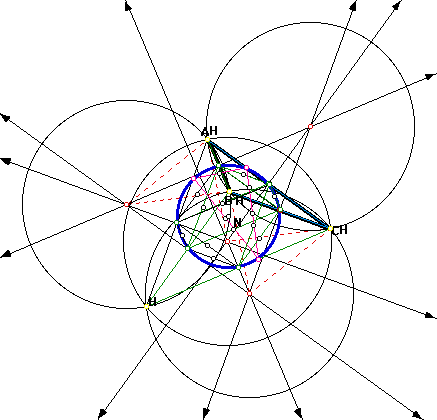
What can be said for all these discoveries?

 

 

Return