

Consider the equation y = a sin(bx + c) for different values of a
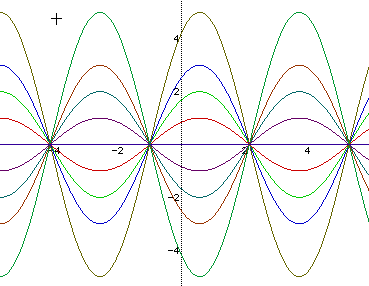
The value of a determines the amplitude of the wave. For example, when a = 2 the sine function oscillates between +2 and -2; when a=5 the function oscillates between +5 and -5. When a is negative we get a symmetry reflection of the function in the y=0 axis. When a =0 the function is then represented by the line y=0 i.e. there is no displacement.
Now let us consider the function when only b varies:
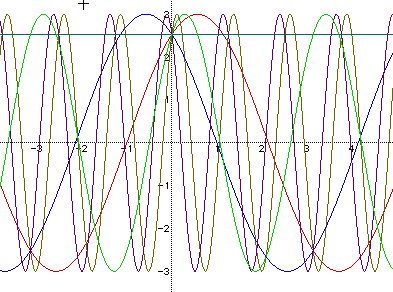
This graph shows that by varying b only the period of the wave changes. If we consider those graphs when b is positive, we notice that as b increases the wavelength of the wave decreases but the frequency increases. When negative values of b are compared with the corresponding positive values we notice a phase shift in the waves.
We will now examine when only c varies:
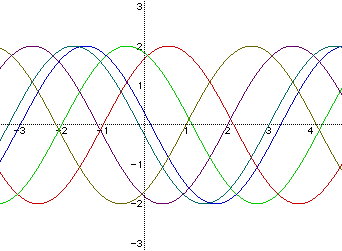
We notice that as c increases for positive values, the waves experiences a phase shift to the left. When c increases for negative values, the wave shifts to the right.