

Consider the equation when a=1
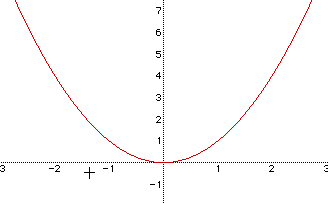
We see that the parabola has symmetry reflection about the y-axis and a minimum value of 0.
Let us now consider equations when a = 1, 2, 3, 4 ,5 and observe what happens to the graphs.
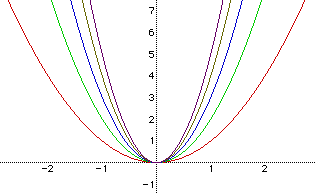
We notice that a = 1 produces the widest graph. As a increases the parabolas get thinner and thinner. The graphs all show symmetry reflection in the y-axis and a minimum value of 0.
We will now compare the graphs for a = 1 and a = -1.
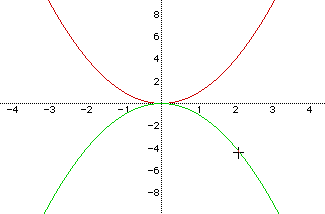
We see that there is a reflection of the graphs in the line y = 0. When a= 1 the parabola opens up and has a minimum value of 0 but when a = -1 the parabola opens down and has a maximum value of 0.
Let us now consider other values for a that are less than 0. For example a = -1, -2, -3 , -4, -5.
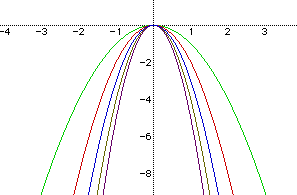
We see that a = -1 produces the widest graph. The parabolas get thinner as a gets smaller. Although, the graphs maintain symmetry reflection in the y-axis, there is a maximum value of 0.
If we now combine the graphs using values for a = -3, -2, -1, 0, 1, 2, 3
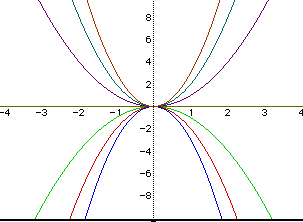
We notice that the graphs are reflected in the line y = 0 i.e. when a =0 and have symmetry reflection in the line x = 0. For positive values of a the parabolas open up and have a minimum value of 0. Whereas, for negative values of a the parabolas open down and have a maximum value of 0.