

To investigate the relationship between two triangles with the second triangle having as its sides the lengths of the three medians of the first triangle.
Construct the triangle ABC and its medians AF, BD, and CE. Construct the second triangle ECI with the three sides having the lengths of the three medians from the first triangle.
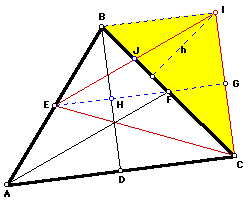
EI is congruent to AF', IC is congruent to BD, EC is congruent to EC
It was found by measurement that (Area EIC)/ (Area ABC ) = 0.75
To prove that the area of a triangle having its sides the lengths of the three medians of a first triangle is three-quarters the area of the first triangle.
By construction complete the parallelogram BDCI.
Triangle BIC and triangle JIC both have the same height (h) since they have a common base and vertex.
BF and FC are congruent from the definition of a mid-point.
BJ = 1/2 BF and therefore JC = 3/4 BC since the diagonals of a parallelogram bisect each other.
Area JIC = 1/2 JC x h, using the formula for the area of a triangle.
Area EIC = 2 x Area JIC = 2 x 1/2 JC x h = JCh , since JC is a median of triangle EIC.
Area EIC = JCh = 3/4 BCh by substitution
Area BIC = 1/2 BC x h, using formula for the area of a triangle.
Area BIC = Area BDC since BC is a diagonal of parallelogram BDCI.
Area ABC = 2 x Area BDC = 2 x 1/2 BC x h = BCh since BD is a median of triangle ABC and by substitution.
We have found that Area EIC = 3/4 BCh and the Area ABC = BCh
Hence Area EIC = 3/4(Area ABC)