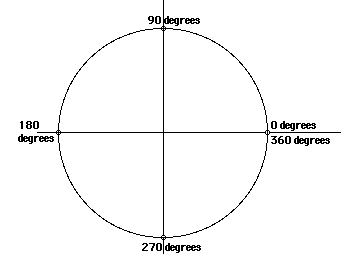
To measure angles, it is convenient to use the circumference of a circle. A full revolution (counterclockwise) corresponds to 360 degrees, a half revolution to 180 degrees, a quarter revolution to 90 degrees, and so on.
Recall that in a coordinate system there are four quadrants, numbered I, II, III, and IV. The diagram below shows which angles betwee 0 degrees and 360 degrees lie in each of the four quadrants.
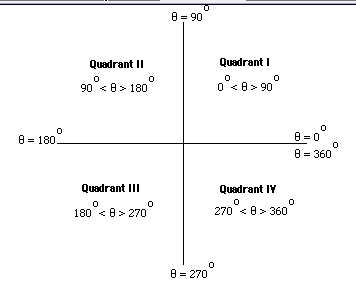
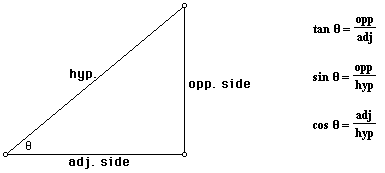
Below is a right triangle, one of whose angles is labeled 
. The three sides
of the triangle are the hypotenuse, the opposite side (the
side opposite the angle ), and the adjacent side (the
side adjacent to the angle ). Using the lengths of these three sides,
we can form three ratios that define three trigonometric functions of the
acute angle .
We can now use this information to investigate these three trigonometric functions.
Click HERE to investigate the trigonometric functions.