

An open box is made by cutting squares out of the corners of a piece of cardboard that is 5 cm by 8 cm, as shown in the diagram below. The edge of each cut-out square is x cm.
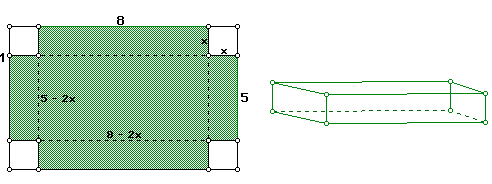
What is the volume of the box? Find the volume when x = 0.5 cm, x = 1 cm, x = 1.5 cm, and x = 2 cm. What value of x will produce a box of maximum volume?
Click HERE to explore this question.
The volume of a rectangular box is equal to the product of its height, width, and height. From the diagram, the length is 8 -2x, the width is 5 - 2x, and the height is x. Thus, the volume of the box is
When x = 0.5 cm, the volume of the box is
![]()
When x = 1 cm, the volume of the box is
![]()
You can try several values of x to see if you can produce a box that has a maximum volume.
Another way would be to draw a graph of the polynomial ![]()
Click Here to explore this option.