

When two or more lines intersect in one point, the lines are said to be concurrent.
Given triangle NOM, with lines j, k, and l representing the altitudes, we choose axes and coordinates as shown.
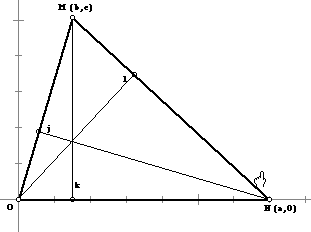
The equation of the line k is x = b.
Since the slope of MN is c / (b - a), the slope of line l is (a - b) / c.
The equation of line l is y = [(a - b) / c] x since the y - intercept is O. The equation follows from the Slope - Intercept Form Theorem.
Lines k and l intersect where x = b any = [(a - b)/c] b, or
On l, when x = b, y = [(a - b)/c] x = [(a - b)/c] b, or
Since the slope of OM = c/b, the slope of line j is -b/c. The equation of line j is y = (-b/c)(x - a) since j passes through (a, 0). The equation follows from the Point - Slope Form Theorem.
Lines k and j intersect where x = b and y = (-b/c)(b - a), or
On j, when x = b, y = (-b/c)(x - a) = (-b/c)(b - a), or
The three altitude lines intersect in a point. The coordinates of this point is