A. Consider any triangle ABC. Point P lies inside the triangle with lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F respectively.

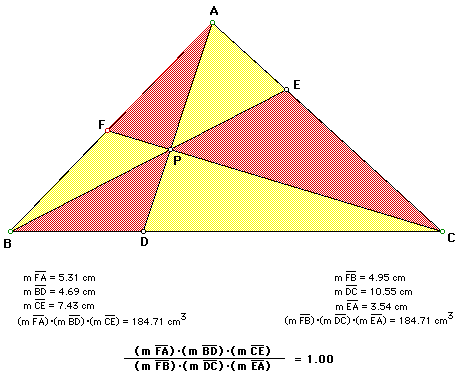
My explorations show that this relationship holds for any triangle ABC with the point P inside the triangle.

B. To prove that

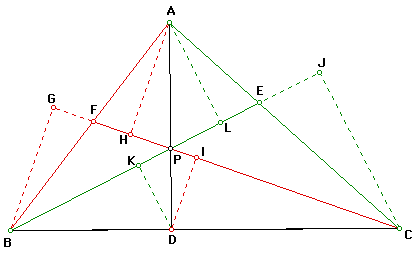
Click HERE to observe that as P moves outside of the triangle

C. To show that when P is inside the triangle ABC, the ratio of the areas of ABC and DEF is always greater than or equal to 4.

If F, E, and D are the mid-points of AB, AC, and BC respectively then triangle ABC is divided into four equal triangles, one of which is DEF. Triangle DEF is 1/4 of triangle ABC.

Therefore, (area of ABC)/(area of DEF) = 4

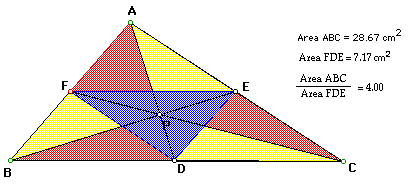
As P moves around inside the triangle ABC and F, E, and D are no longer mid-points of AB, AC, and BC respectively, the area of triangle DEF is less than 1/4 of the area of triangle ABC. This implies that

(area of ABC)/(area of DEF) > 4

Click HERE to observe the ratio of the areas as P moves inside the triangle.