Consider the problem of finding two linear functions f and g such that fg=h, and h is tangent to f at one point and g at one point.

When a student is given a problem such as this one, no numbers given and none to find, one of two things may happen. Either the student will become intensely interested in finding an "answer" or jump ship and run. Of course as a teacher we are worried about every student but, those that feel uncomfortable with a problem are of special concern to us. A teacher can't quite convince a student that something is interesting but, can convince them that, with open ended problems such as this one, it is the trying that produces the learning rather than the finding of the "right" answer. Support and encouragement will yield student observations about the relationship between lines and parabolas that no amount of telling can produce. So support and encourage as students pass through the phases of discovery associated with this problem. You will be excited by the richness of the results that they generate.

In considering this question there are likely to be three phases through which a student will pass.

Phase 1: Investigation to find an answer.

Phase 2: Investigation to find a family of solutions or a general solution.

Phase 3: A quest to prove or verify that the general solution found is correct.

The following write up will explore each of the three phases of investigation. One should note that not all students will experience all three phases.

Phase 1: INVESTIGATION or TRIAL AND ERROR

Without thinking very much about the graph of the linear equations or the graph of the parabola that is produced when the product of the linear functions is graphed, an example much like this one is likely to result.

FIRST TRY: f(x) = 2x + 1, g(x) = 3x + 1, h(x) = (2x+1)(3x+1)

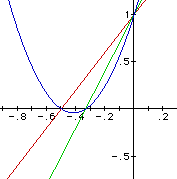
Once this graph is analyzed it becomes fairly clear that both lines, f and g, can not have positive slopes, so

SECOND TRY: f(x) = 2x+1, g(x) = -3x + 1, h(x) = (2x+1)(-3x+1)

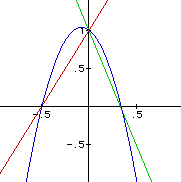
This is much closer but, it still is not tangent to the parabola. Now the symmetry of the parabola may be used to inform the selection of m.

If the student notes, that the slope of the parabola to the left of the vertex is the opposite of the slope to the right, an example such as the next one may be generated.

THIRD TRY: f(x) = 2x+1, g(x) = -2x + 1, h(x) = (2x+1)(-2x+1)

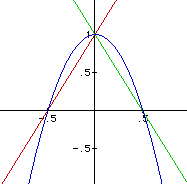
Wow! This is really close! The only problem seems to be the y-intercept. With a bit of tinkering (changing the y-intercept of g) one can find a solution.

FOURTH TRY: f(x) = 2x+1, g(x) = -2x, h(x) = (2x+1)(-2x)

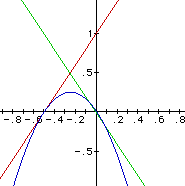
Yeah! At last a solution!

Phase 2: FINDING A GENERAL SOLUTION

When a student has determined a solution for the given problem they feel great! As they should, this process of discovery is no simple task. Some students will be satisfied with finding an answer while others will suddenly think about what all the solutions might look like. For this student the trial and error used in phase 1 is just the beginning. Now in a quest to discover a general solution the student tries to find other solutions that satify the given conditions. If a student had to generate solutions without the use of the technology the number of solutions that could be generated might not produce a "generalization." The speed of the trial and error that can be attained on the computer make phase 2 accomplishable.

After generating more examples of solutions the student will generate a general family of solutions

GENERAL SOLUTION:

f(x) = mx + b, g(x) = -(mx + b-1)

or

f(x) = -(mx + b), g(x) =mx + b+1

This is a fantastic moment! The student generating such a solution has created a mathematical formula from connection that they made through investigation.

Phase 3: Proof

When a general solution is generated, the next question might be "Is it right?" The student should be encouraged to find out. The investigations that have been done so far should inform the proof of the solution. If the student tries to prove the general solution without using observations made in phase 1 (trial and error) they may be in for difficult time.

One can observe, in the course of investigations, that the x-intercepts of the parabola are the points at which the parabola and the lines are tangent. This observation is very useful in reducing the complexity of the proof.

Assuming that the slope of f and g are opposite, f(x) = mx+b , g(x) = - (mx+c), and h(x) = - (mx+b)(mx+c) we can prove that c = b+1 or c = b - 1 depending on the sign of m.

Proof: Using h'(x) = slope of the tangent line to the curve = + or - m and solving for x we find

*.

Then using the zero product property to find the x-intercepts of the parabola we find

**.

Now since we have seen that the x-intercepts of h(x) are the points at which h is tangent to f and g we can set *= ** which yields:

and .

Solving for c in either equation shows that c = b+1 or b-1.

Hence, if f(x) = mx+b then g(x) = - (mx + b-1) and if f(x) = - (mx+b) then g(x) = (mx+ b+1).

APPLICATION

This problem can help to motivate a number of concepts that are often "told."

Application 1: Zero product property

After a number of attempts in phase 1 of the problem solving process the student will no double notice that the x-intercepts of the parabola are the x-intercepts of the lines. Even if the student is unable to "solve" the posed problem the connection between the x-intercepts of the quadratic and the x-intercepts of the factors of the quadratic can be capitalized on. The graphical understanding leads to an algebraic understanding so that student can generate an example like the following.

h(x) = (x+2)(x- 3) = 0 only if x+2 = 0 and x-3 = 0.

Return