Consider the graph of the circle

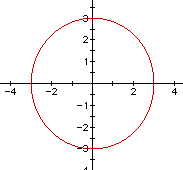
The circle could be considered a special case of the equation

with n equal to zero. In fact we can generate special cases of ellipses, hyperbolas, and even parallel lines in one case, by using this equation.

After a bit of investigation using various values of n, we find that when 0 < n < 2 and 0 > n> -2 , the graph of

is always an ellipse whose major axis the the line y = - x. For example let n = 1, then

has the following graph

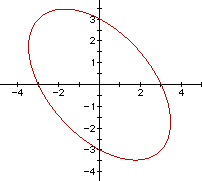
You can even change the orientation of the ellipse by changing n.

Suppose n = -1 , then we have the equation

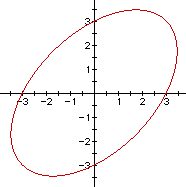
So what happens when -2 < n > 2 , then the graph is always a hyperbola.

If n > 2 , then the hyperbola is symmetric with the lines y = x and y = -x.

For example let n =3

has the following graph

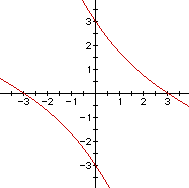
And as with the ellipse, you can change the orientation of the hyperbola by changing n. If n < -2 then the hyperbola is still symmetric with respect to the lines y = x and y = - x but graph does not intersect the line y = x.

Suppose n = -3 , then we have the equation

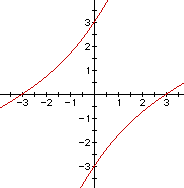
Interestingly enough one can generate parallel lines given the equation

You guessed it, if n = 2 , then the graph of the equation

is a system of parallel lines.

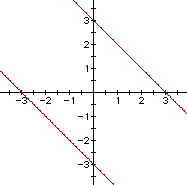
But you might have guessed this already since if

Similarly, if n = -2, lines are generated.

x and y -intercepts

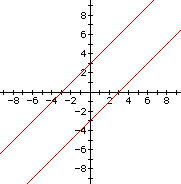
So in looking at the graphs generated by the equation

what are the commonalities? Upon inspection of the graphs generated for each of the following cases

Case 1: n = 0

Case 2: -2 < n < 0 and 0 < n < 2

Case 3: -2 < n > 2

Case 4: n = 2 and n = -2

it can be seen that the x-intercepts for the graphs are -3, 3 and the y-intercepts are -3 and 3.

symmetry

We can also see by inspection that y = x and y = - x are lines of symmetry for the graphs of the equations generated for each of the cases deliniated above.

---

An Application

The family of equations generated by

is extremely useful in connecting the information learned about lines to second degree equations.

Consider building a family of second degree equations from the linear equations x + y = 3, x - y = 3.

Have the students find all the possible equations generated by these three lines.

Case 1: (x+y)(x+y) = 9

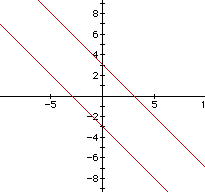
Case 2: (x+y)(x- y) = 9

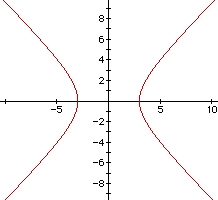
Case 3: (x- y)(x- y) = 9

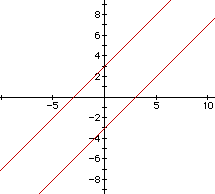
Now what happens if you change the coefficients of x and y for the lines x+y =3 and x+y = -3? Can you ever get an ellipse?

Return