The genetic approach developed below was demonstrated in the article entitled Teaching Logarithms Via Their History by C. Toumasis, published in School Science and Mathematics (1993) Volume 8. The area under a curve approach can be seen in the School Mathematics Study Group (SMSG) text, Intermediate Mathematics.
Consider the following table of numbers. The first column contains the first twenty terms of an arithmetic series while the second column contains the first twenty terms of a geometric series.
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| 6 | 64 |
| 7 | 128 |
| 8 | 256 |
| 9 | 512 |
| 10 | 1024 |
| 11 | 2048 |
| 12 | 4096 |
| 13 | 8192 |
| 14 | 16384 |
| 15 | 32768 |
| 16 | 65536 |
| 17 | 131072 |
| 18 | 262144 |
| 19 | 524288 |
Do you see any relationship between these two series? Click HERE to explore using an excel worksheet.
 |
 |
 |
 |
 |
 |
 |
 |
One way to describe the correspondence would be 
. Or we could
write 
, where n is any positive integer. Where "log" stands for
logarithm and is a fundamental property of logarithms. Other properties
can be discovered by looking at the relationships betwen the terms in the
sequence. For example notice that 
, where n and m are positive integers.
Using the logarithm idea from above we can see that 
= m + n = 
.
Now, substituting 
we have another fundamental property of logarithms,
namely log(xy) = log x + log y.
The term logarithm signifys the ratio, r , used in the geometric sequence (2 was used in the geometric sequence above). In general we write
.There are other properties of logarithms. Can you derive them?
Consider the function 
whose graph when k = 1 is shown below.
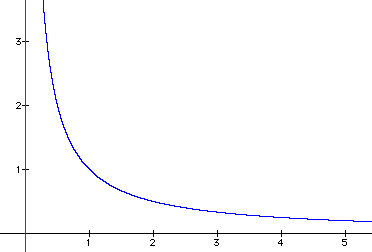
The logarithm function for x > 0 can be defined as the area, A, bounded
by the curve , the x-axis, x = 1, and the vertical line through the
point (x, 0) hence
So for example if we woul like to find the log 2 we would simply calculate
the area under the curve on the interval [1,2].
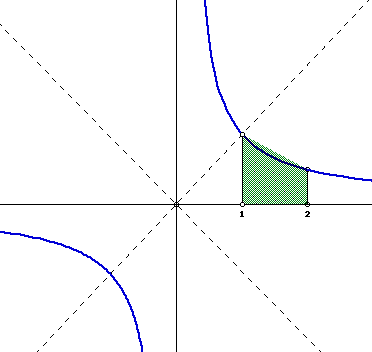
As you can see the green area is trapezoidal and hence easy to calculate
using the formula 
.
You can also see that the area of the trapezoid is not the area under the curve, but just a bit more. That could throw our approximation off. How might you get a better approximation?
Before the calculator was invented people need ways to do complicated numerical calculations quickly. Suppose that you were asked to calculate the following expression by hand.
The ten doesn't look too bad, but that three to the forty-seventh power is rough! The laws of logarithms helped with calculations such as these. The expression above can be simplified into much easier calculation
.In order to compute horrible looking numerical calculations students and scientists used slide rules. What appears below is a base 2 slide rule.
You can use the slide rule and see a demonstration by clicking HERE. Try it out!