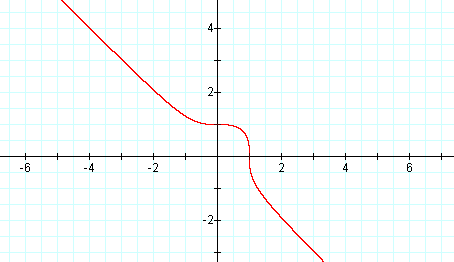
Graph (b) x3 + y3 = 1
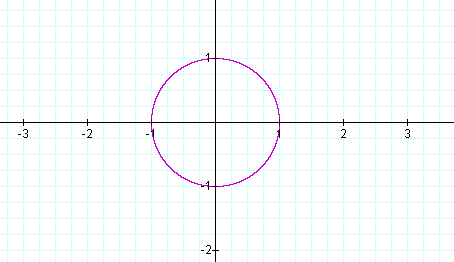
Graph (c) x4 + y4 = 1
Graph (d) x5 + y5 = 1
What do you expect for the graph of x24 + y24 = 1 or x25 + y25 = 1?
I believe that the graph of x24 + y24 = 1 will have a similar pattern to that of figure c, while the graph of x25 + y25 = 1 will have a similar pattern to that of figures d. Let’s see!!
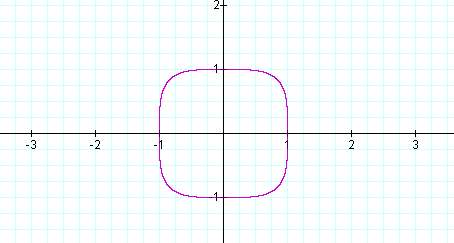
The graph of x24 + y24 = 1 looks like the figure below.
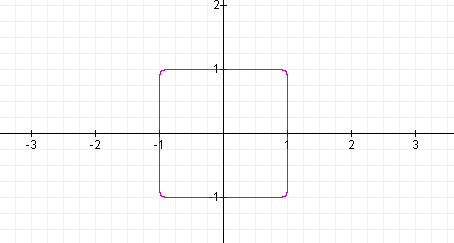
Using the laws of exponents, x24 + y24 = 1 can be written as (x6)4 + (y6)4=1. Note that x4 + y4 = 1 and (x6)4 + (y6)4=1 resemble one another. Below, both equations are graphed simultaneously.
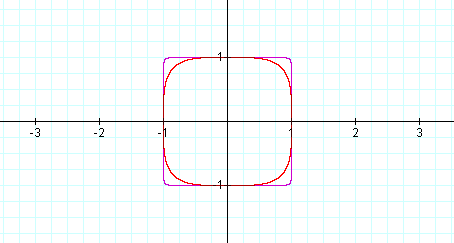
While the graphs are different, they share a close resemblance to one another and share common x- and y-intercepts. The graph of x4 + y4 = 1(in red) is rounder than x24 + y24 = 1(in purple). I graphed several equations of the type xn + yn = 1 using even numbered exponents. Each graph had likeness to a circle and/or quadrilateral .The graph, at times, seemed to be a hybrid of the two. The higher the even exponent, the more like a quadrilateral (square), the graph resembled. The lower the even exponent, the more round the corners became. At x100 + y100 = 1, the graph was a square. As the even numbered exponent increased or decreased respectively, differences were noted in the sharp or rounded nature of the arcs or corners or each graph.
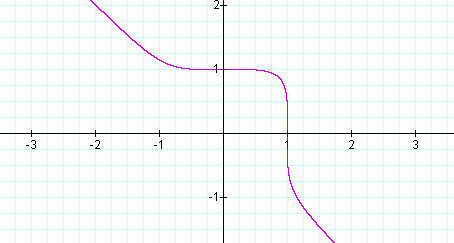
Below, the graph of x25 + y25 = 1 (in purple) and x5 + y5 = 1 (in red) have been drawn simultaneously. Note the similarities.
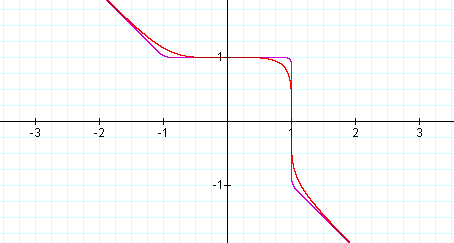
The general pattern of each graph is the same. After graphing several equations of the type xn + yn = 1, where the exponents are the same and odd, the graph of the equation always had the same pattern. The differences can be seen in the rounded or sharp nature of the concavity of the graph.