EMAT 6680
Assignment 4
Stephanie K. Lewis
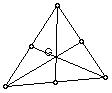
1. Centroid Construction

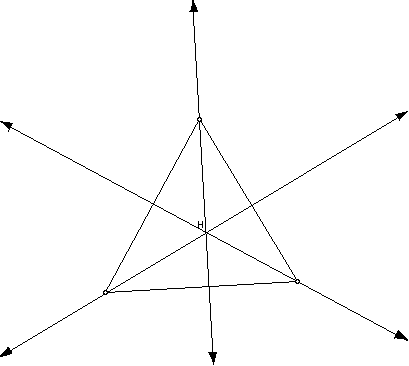
2. Orthocenter Construction
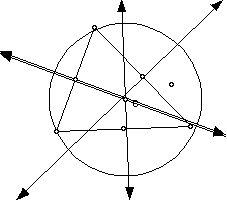
3. Construct the Circumcenter C. (It is the center of the circumcircle).
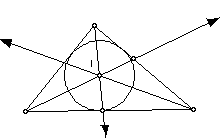
4. Incenter (I) Construction.
5. Use GSP to construct G. H, C, and I for the same triangle.
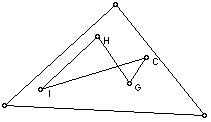
On this particular construction, I manipulated the points inside, and outside of the triangle. I was uncertain as to whether you wanted the vertices of the triangle to be points H, C, G, and I be a point on one of the segments. In any event, I tried this construction several ways. If the points are in side of the triangle, and atleast three points are connected, then we can get variations of triangles. If no points are connected, then of course, we are simply moving points around.
6. Medial Triangle Construction
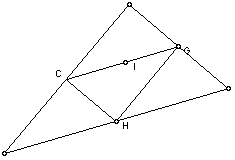
7. Orthic Triangle Construction
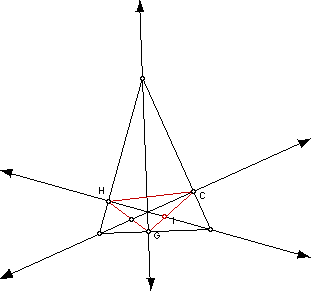
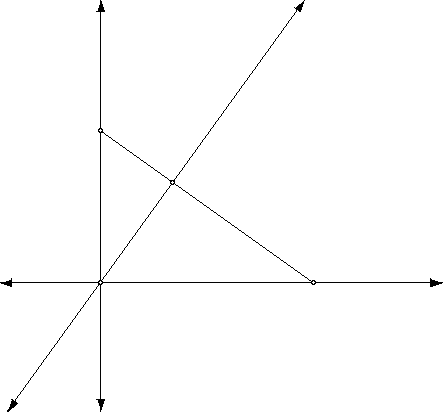
After extending the orthic triangle concept to right and obtuse triangle, I found that a triangle cannot be constructed from the feet of the three altitudes because only one foot of an altitude can be gotten!!! Check out the following drawing of a right triangle.
8. If triangles are similar, then their perimeters should be proportional to any pair of corresponding sides. After all, triangle similarity theorems are built on proportionality. With that in mind, I tested my hypothesis. My findings are below.
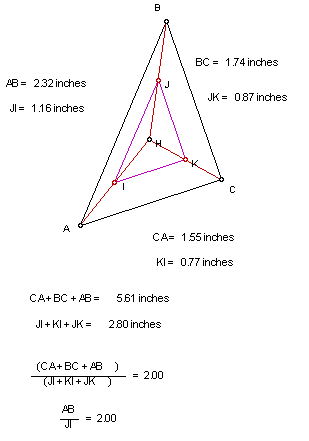
Since the ratio of the perimeter of D ABC and D IJK are proportional to AB and IJ, as well as the other corresponding sides, then the triangles are indeed similar.