Stephanie K. Lewis
Assignment 8 #8 (A8#8)
EMAT 6680
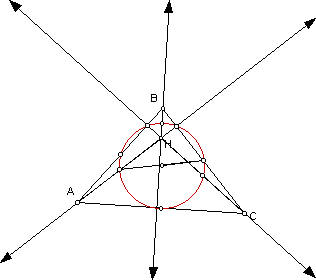
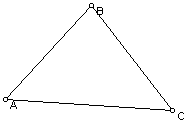
1. Construct any triangle ABC.

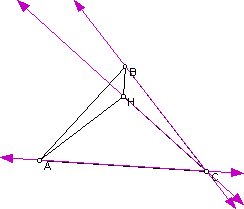
2. Construct the Orthocenter H of triangle ABC.
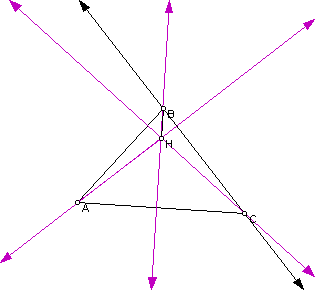
3. Construct the Orthocenter of triangle HBC.
The three altitude of triangle HBC intersect at point A.
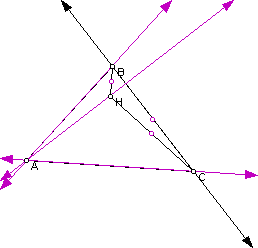
4. Construct the Orthocenter of triangle HAB.
The orthocenter of triangle HAB is point C.
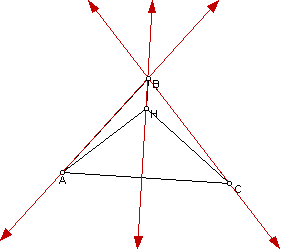
5. Construct the Orthocenter of triangle HAC.
The orthocenter of triangle HAC is point B.
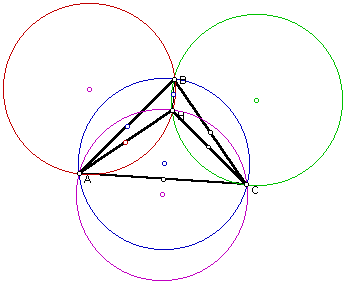
6. Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC.
The circumcircle of each triangle is highlighted as follows:
The circumcircle of triangle ABC is highlighted in blue.
The circumcircle of triangle HBC is highlighted in green.
The circumcircle of triangle HAB is highlighted in red.
The circumcircle of triangle HAC is highlighted in purple.
Circumcircles of triangles ABC, HBC, HAB, and HAC.
7. Conjecture? Proof?
After some investigation of the circumcircle diagram, it appeared that the radius of each of the circles was similar. Upon measuring them, the radii of each were indeed equal.
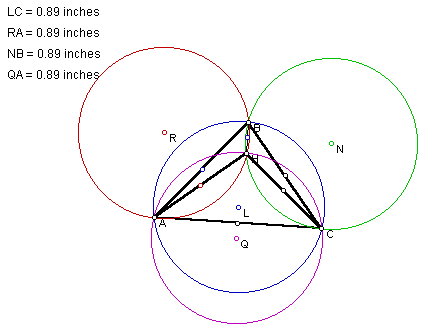
Additionally, each chord in the various circles joining the points of tangency (of the two tangent lines) from a point outside the circle, are the vertices of the given triangles. The chords themselves, are the legs of sides of the given triangle.
8. Construct the nine point circles for triangles ABC, HBC, HAC, and HAB.
Nine point circle for triangle ABC.