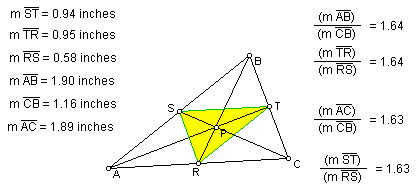
1a. Let triangle ABC be any triangle. Then, if P is any point in the plane, the triangle formed by constructing perpendiculars to the sides of ABC (extended if necessary), locate three points R, S, and T that are the intersections. Triangle RST is the Pedal Triangle for Pedal Point P.
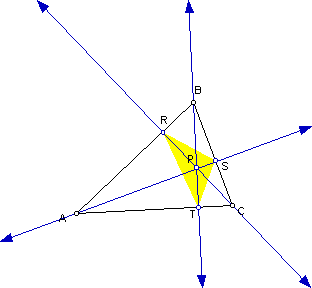
2. What if pedal point P is the centroid of triangle ABC?
If pedal point P is the centroid of triangle ABC, then the triangle formed, triangle TRS would be similar. That is, the ratio of the corresponging sides of each traingle would be congruent. Upon investigation, and calculation, I found that that was indeed the case.