

A parametric curve in the plane is a pair of functions
x=f(t)
y=f(t)
where the two continuous functions define ordered pairs (x,y). The two functions are normally called parametric equations of a curve, and the curve is dependent upon the range of t. We will be exploring the parametric equations
x=cos t
y=sin t
as well as variations of these equations. In these cases,
![]() .
.
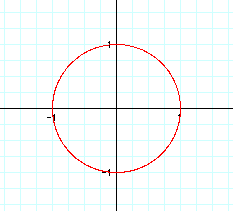
Notice that these, the simplest of the parametric equations involving sine and cosine of t whenever t is between 0 and 6.28. Of course this graph is often called the unit circle from which all kinds of trigonometric values may be derived. Before the onset of the scientific calculator, it was necessary to remember sines and cosines for particular values of t in order to use trigonometry to its potential. Of course, these significant values as well as all others are easily attainable by the push of the right combinations of buttons on a scientific or graphing calculator today.
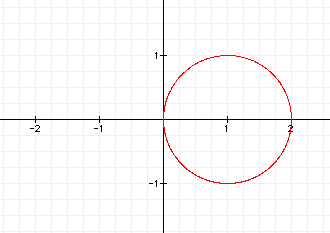
These parametric equations also give us the ability to define a circle in a way different from that of the variations we could use on a equation involving x and y. We can also explore moving this circle around the plane by adding or subtracting values to either cos t or sin t. For example,
x=cos t +1
y=sin t
yields a graph that moves the circle to the right of its existing place by one unit.
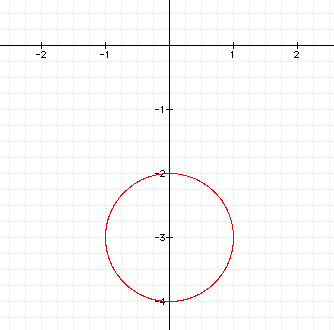
Subtracting from the value of sine by the following value yields a graph that is 3 units down from the original position:
x=cos t
y=sin t-3
Naturally, we can continue this process of moving around the unit circle by continuing to add or subtract values from the parametric equations. In fact, we can make the center of our circle be anywhere on the plane we would like, simply by appropriately adding or subtracting these values. If we wanted to place our circle with a center of (-2,4), we would change our parametric equations to be
x=cos t -2
y=sin t+4.
Here is that graph:
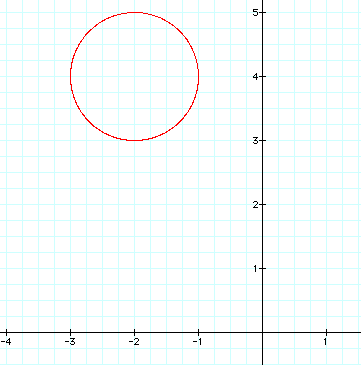
The result is quite significant since this method allows for placing a graph in a particular location with great ease of understanding and implementation.
Now, in these examples we have already discussed, we have moved the circle around the plane, but we have not varied the size of the circle. Let's explore this area of changing the radius of the circle with the same ease as that of its center. Observe the graph of the following pair of parametric equations:
x=2cos t
y=sin t.
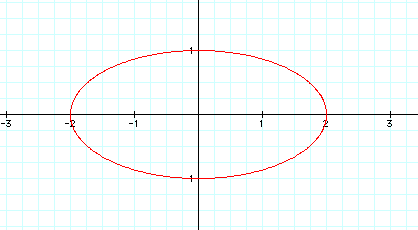
It is obvious that we no longer have a circle, rather an enlongated circle otherwise known as an ellipse. This opens up an entirely new set of ideas of easily manipulating the graphs of now not only circles but also ellipses. It stands to reason that if we want to keep our graph in circular form, we need to multiply both cosine t and sine t by the same factor. Look at the graph now that we have changed both parts of the parametric equations:
x=3 cos t
y=3 sin t
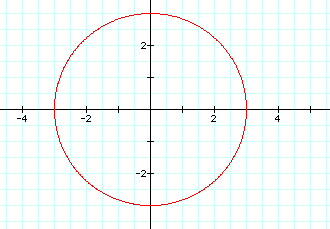
Our circle now has a radius of 3 which of course is the coefficient on the two functions. Once again, with ease we can now make a circle of any radius and with its center at any place on the coordinate axis. With the parametric equations written in general form, we find that
x = a cos t + m
y = a sin t + n
yields a circle with radius a and centered at (m,n).
But what if the coefficients on the functions are different values? We just showed that if
x = 2 cos t
y = sin t,
then only the cosines of t are multiplied by 2, thus making the graph an ellipse. We then have the understanding to create ellipses of any dimensions we would like. These parametric equations will be of the form
x=a cos t
y=b sin t
Look at several graphs simultaneously:
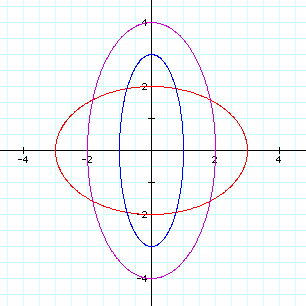
red ellipse: x=3 cos t
y=2 sin t
purple ellipse: x=-2 cos t
y=4 sin t
blue ellipse: x=cos t
y=3 sin t
It makes sense that to enlongate the graph along the x-axis, we must use a>b. Conversely, to enlongate the graph along the y-axis, a<b. This method of using parametric equations to explore ellipses shows the ease with which the graphs can be changed and manipulated. We also would like to point out that, as in the case of circles, the "center" of the ellipse may be moved by adding on values to the cosine of t and the sine of t, in the form of
x = a cos t + m
y = b sin t + n
where the "center" is at (m,n).
Finally, let's investigate parametric equations of the form
x = cos (at)
y = sin (bt)
![]() .
.
Look at a change in a=1 and b=2:
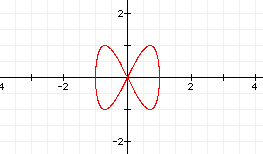
Now let's look at multiple sets of equations:
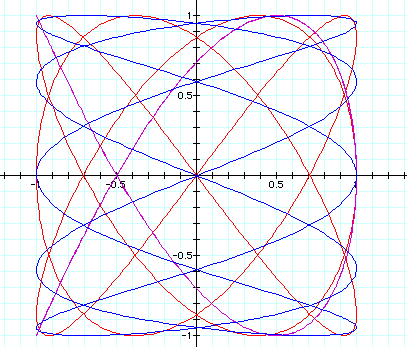
red graph: x = cos (3t)
y = sin (4t)
purple graph: x = cos (2t)
y = sin (3t)
blue graph: x = cos (5t)
y = sin (2t)
Even though these graphs appear to be a tangle of strings, these graphs do have some rhyme and reason. The value of a tells the number of intersection points horizontally across the top of the graph, and the value of b describes the number of intersection points and endpoints vertically down the side of the graph. Of course, all of the graphs share the common point of (0,0), and are found within the same confines of
-1 < x < 1 and -1 < y < 1.
These are particularly interesting graphs since they are far less predictable from the others in our series of parametric equations.