

In this assignment, we are making discoveries about polar equations. Polar equations are based on a number of variables with the main parameters of ø, for the various angles of a circle, and r, for the length of the radius of the circle. The "pole" is the location of a line when ø is 0 radians for any positive value of r. A polar point is of the form (r,ø) and a polar equation graphs a series of these polar points according to the function of the equation on a polar graph.
INVESTIGATION #1
We want to look at what happens to the graph of
r = a + bcos(kø)
for a=b, a>b, and a<b and when k is in integer values between 0 and 6.28 radians.
Let's look at the function when a=b=1 and k=1:
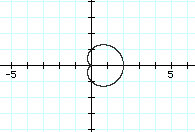
This is a fairly interesting graph of r=1+1cos(ø). It appears to be a cardioid, obviously coming to a point at the origin. But as we change the value of a=b=2, we see the graph become:
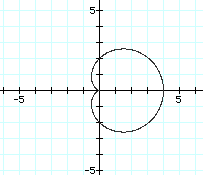
This cardioid is larger than the previous one with a=b=1, but the graphs look similar. After investigating changing the values of a=b=3,4,5, 6,-1, -2, -3, and -4, we think we can make some conjectures about the nature of the graphs. The point of the cardioid is at (0,0) with the graph being symmetric about the x-axis. The bulk of the graph is to the right of the y-axis when a and b are positive and to the left of the y-axis when a and b are negative. Look at the graph of
r=-3-3cos(ø)
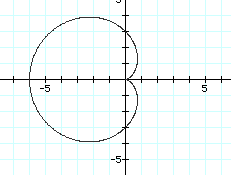
Noticably, the graph is reflected around the y-axis from when a=b=3. Also, the x-intercepts of the cardioid are the ordered pairs (-(a+b),0) and (0,0). The cardioid has y-intercepts of (0,3) and (0,-3), the values for a and b and their opposites.
When we look at r=a+bsin(ø), we find that the graph has similar characteristics, but the symmetry is of the y-axis instead of the x-axis. Observe,
r=4+4sin(ø)
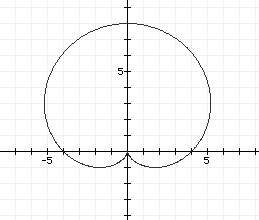
Clearly, the same types of characteristics occur for this graph as well. The y-intercept of the cardioid is again the ordered pair (0,(a+b)) or, in this case, (0,8), and the x-intercepts are at (-a,0) and (a,0) or, in this case, (-4,0) and (4,0). In summary, when a=b in the equation r=a+bcos(kt) or r=a+bsin(kt) and k=1, a cardioid is the graph with quite predictible characteristics.
All of the graphs investigated so far , we have been using k=1. Now let's see what happens as the value of k changes to other integer values. Look at the graph of
r=2+2cos(2ø)
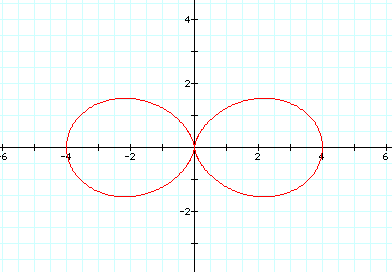
It is obvious that we no longer have a cardioid. Instead, we have a "k-leaf" rose with x-intercepts of (-(a+b), 0), (0,0), and ((a+b),0) or, in this case, (-4,0), (0,0), and (4,0).
Now let's see what happens as we look at several different graphs simultaneously as k changes integer values:
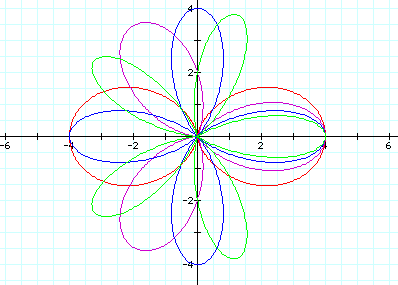
r=2+2cos(2ø) (red)
r=2+2cos(3ø) (purple)
r=2+2cos(4ø) (blue)
r=2+2cos(5ø) (green)
The value of k dictates the number of leaves in the rose formed by the graph. Since this graph involves cosine of kø, the graph is symmetric about the x-axis. Once again, the x-intercepts are (-(a+b),0), (0,0), and ((a+b),0). A new characteristic emerges since all of the leaves are not centered on an axis. Thus, the length of each leaf is expressed as the quantity (a+b).
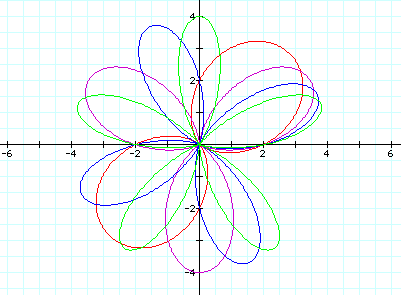
Whenever the equation is changed to r=2+2sin(kø), the graph has all the same characteristics with the exception that it is symmetric about the y-axis instead and the y-intercepts are of the form (0,-(a+b)), (0,0), and (0,(a+b)):
Let's look at some graphs where a<b in r=a+bcosø:
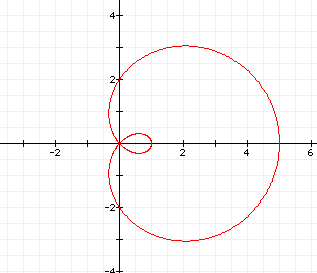
r=2+3cosø
Clearly, the cardioid shape of a=b has developed a new twist of a loop whenever a<b. Look at multiple graphs of this nature:
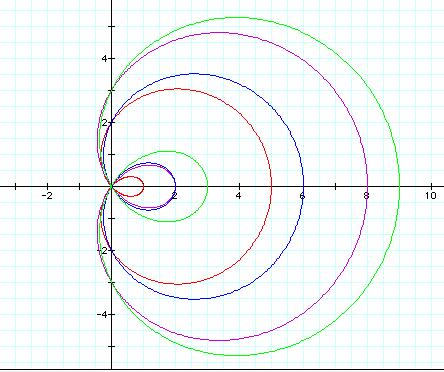
r=2+3cosø (red)
r=3+5cosø (purple)
r=2+4cosø (blue)
r=3+6cosø (green)
In all of the graphs shown above and in general, the loop is of the length (b-a) and the length of the lemiscon is (a+b). They all share the point (0,0). The y-intercepts are of the form (0,-a) and (0,a). Look at the graphs of this same form whenever negative values of a and b are used:
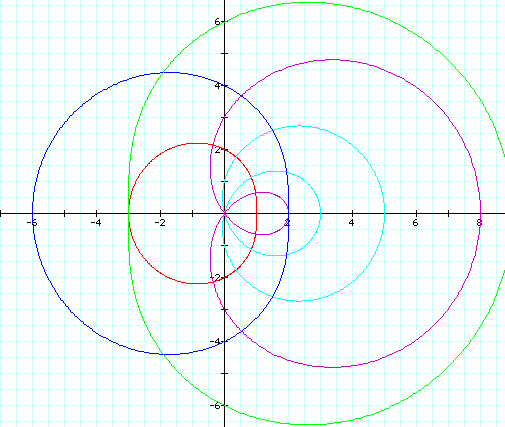
r=(-2)+(-1)cosø (red)
r=(-3)+(5)cosø (purple)
r=(-4)+(-2)cosø (blue)
r=(-6)+(-3)cosø (green)
r=(-1)+(4)cosø (light blue)
Remember that we were trying to keep a<b. And in each of the equations given above, the value of a is less than the value of b. Whenever a is negative and b is positive, the graphs behave as those we have already explored, that of a lemiscon with a loop. But look at the graphs whenever both a and b are negative and |a|<|b|. Suddenly the graph develops a "bump" instead of a loop, which is the behavior of the graph if a>b. We thought that the use of negatives would reflect the graph across the y-axis, but their use seems to have no effect. In short, the graph of r=a+bcosø graphs with a loop whenever |a|<|b|. Predictibly, the graphs of r=a+bsinø are similar, but are symmetric about the x-axis.
Now, let's look at this same equation when a>b:
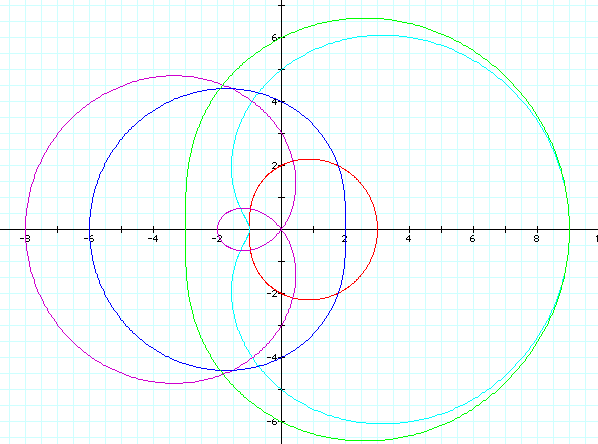
r=(2)+(1)cosø (red)
r=(5)+(4)cosø (light blue)
r=(3)+(-5)cosø (purple)
r=(4)+(-2)cosø (blue)
r=(6)+(3)cosø (green)
As in the previous example, we find that if |a|>|b|, then the graph no longer has a loop. Rather, it has an indention or flattened surface where the loop used to be. Again, in the case of the purple graph, this behaves as does the case of a<b since the graph does not change do to negative values.
Now let's observe these graphs of r=a=bcos(kø) when a>b and k=2:
r=2+1cos(2ø) (red)
r=5+4cos(2ø) (light blue)
r=4+(-2)cos(2ø) (blue)
r=6+3cos(2ø) (green)
We can see that two disconnected loops occur, the blue one turned length-ways about the y-axis since it has a negative value in it. Now let's see what happens whenever k=3,4,5, and 6:
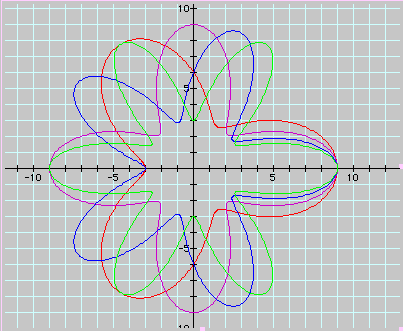
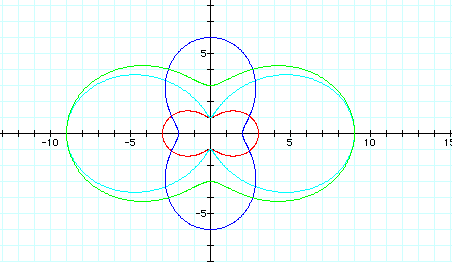
r=6+3cos3ø (red)
r=6+3cos4ø (purple)
r=6+3cos5ø (blue)
r=6+3cos6ø (green)
Notice that as the value of k changes, so does the number of leaves on the rose. If k=3, then there are three leaves; if k=4, then there are four leaves; if k=5, then there are five leaves; and so on. The distance between leaves also is related to the difference between the values of a and b.
In conclusion, the graphs of the equation r=a+bcos(kø) are various. Some create cardioids, some lemiscons with loops or indentions, still others roses with varying numbers of leaves. The graphs involving cosine ø are symmetric about the x-axis while those involving sine ø are symmetric about the y-axis. When k=1, cardioids or lemniscons occur. Whenever k has other integer values, roses occur with k-number of leaves.