

Upon inspecting the various problems for Assignment #2, I found one of the most useful and most intriguing to be that of looking at the various graphs of
which is the more specific case of
where b=1 and c=2. In this problem I will change the various values that a can take on and try to find the different significances therein.
First of all, let's look at the graph when a=2.
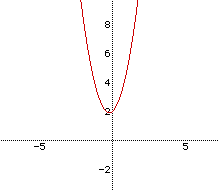
Of course the graph is that of a parabola with its minimum point at (0,2) and it is concave upward. Now let's look at other graphs along with this one when a=3, 4, 5, and 6:
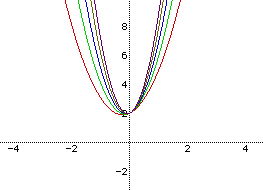
Notice that the minimum point of (0,2) has not changed for any of the graphs. As well, they are all concave upward and centered on the y-axis, just as before when a=2. But the part of the graph that did change is the steepness of the sides of the parabolas. As a increases, the sides of the parabola come into the y-axis more and more. Conversely, as a decreases, the sides of the parabolas flatten out to a point that they can appear almost linear. Speaking of linear, let's look at the graph when a is equal to zero.
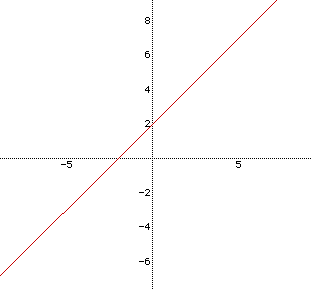
Of course, this graph also has the point (0,2) in the graph but is different from the other graphs in that it is linear instead of parabolic. Therefore, this graph has a constant slope of 1 while, of course, the slopes of the different parabolas is constantly changing. Let's look at the first graphs along with the graph of this linear equation.
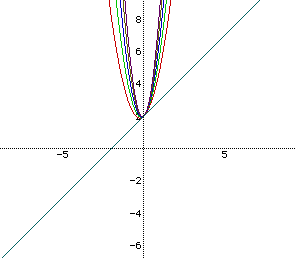
Of course, my best guess is that to make our graphs appear to be concave down, I would need an a value that is negative. Let's look at some of those examples:
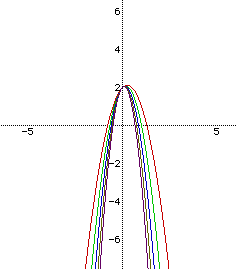
As was expected, we can see that these graphs are reflections of the graphs with a being positive. Once again, they all have the point (0,2) in common again. And once again, they are ever widening as, this time, the absolute value of a is increasing. It also seems clear to me that as the value of a increases to be infinitely large, the parabola will continue to open up and lay down flat, as it were. It would further seem to me, then, that as the value of a decreased to be infinitely small, the parabola will continue to open up from the under side and lay down flat. But we already know that when the value of a is equal to zero, that the "parabola" flattens out to become a line. It does not make sense, then, that the limit of a as it approaches either positive or negative infinity would be zero. But graphically, the picture does make sense.
Now, let's investigate a different function, but approach it in a similar way. Let's look at
In a similar fashion, I will change the value of a and even look at the graph whenever a=0.
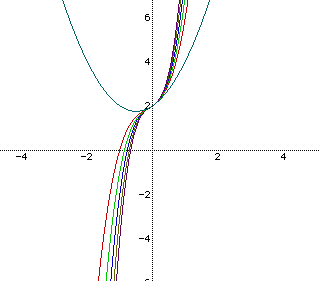
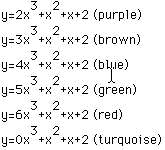
The various graphs of this third degree function as a=2,3,4,5,and6 show ever widening cubics that share the common point (0,2) again as did the parabolic graphs. I can image these cubics continuing to widen as the value of a increases toward positive infinity. And I also anticipated that when a=0, the graph should become parabolic. All of these assumptions come from what I know about the algebra of the functions. However, geometrically, I would have expected the graph to flatten out to be linear whenever a=0 as the two pieces of the graph continue to widen. So I was a bit surprised when the left "arm" of the graph of the cubics jumped above the line y=x+2 in that instance of a=0. I know that in order for this third degree function to be come linear, not only would a have to equal 0, but also the coefficient on the second term would also have to equal zero. Interestingly enough, if a=0 and then the values of the coefficients of the second term continue to change, we get the series of parabolic curves I found in the earlier investigation of the second degree function. Similar results to those of the parabolic graphs occur whenever the third degree function is given values of a equal to negative coeffiecients. The graph is reflected over the x-axis with the same results as a is ever decreasing toward negative infinity. Again, the "arms" of the cubic continue to widen toward the x-axis.
Let''s look at a quartic function with similar coefficient values:
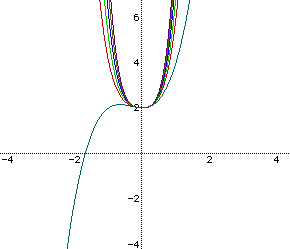
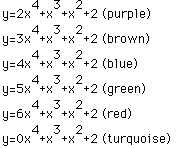
This time, the quartic graphs appear to be parabolic, as do all even degreed functions with coefficients of one on all the lesser degreed terms than the highest degreed term. As did the parabolic graphs, these open up as the value of a continues to increase. If a was given negative values, the same thing would occur in reflection across the x-axis. But whenever a=0, the graph degenerates to the graph of its degree minus one. In turn, this function will degenerate into the next family of curves as a=0 again and again. All of the various functions of the form
finally degenerate into the simplest equation of y=2.