

1. Construct any triangle ABC.
2. Construct the Orthocenter of triangle ABC.
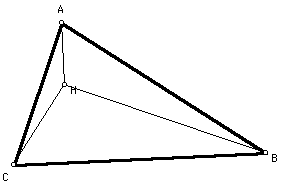
3. Construct the Orthocenter of triangle HBC.
4. Construct the Orthocenter of triangle HAB.
5. Construct the Orthocenter of triangle HAC.
Observations: The orthocenter of triangle HBC is point A; the orthocenter of triangle HAB is point C; and the orthocenter of triangle HAC is point B. Basically the orthocenters formed by the altitudes of the three interior triangles intersect at the three vertices of the original triangle.
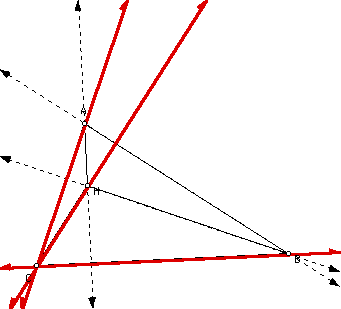
To understand why the observation is true, look at the above picture. The orthocenter of triangle ABH is point C. Lines BH, CH, AH are already altitudes of the original triangle ABC. The altitude of B to line AH, must be line BC, because there is only one perpendicular line to AH through any given point. Line AH is perpendicular to BC by the original construction of orthocenter H. Using this process, you will see that the orthocenter of triangle ABH must be at point C. This also works to explain the orthocenters of the other two triangles. To further investigate this to prove to yourself that this always works, click here.
6. Construct the circumcircles of triangles ABC, HBC, HAB, HAC.
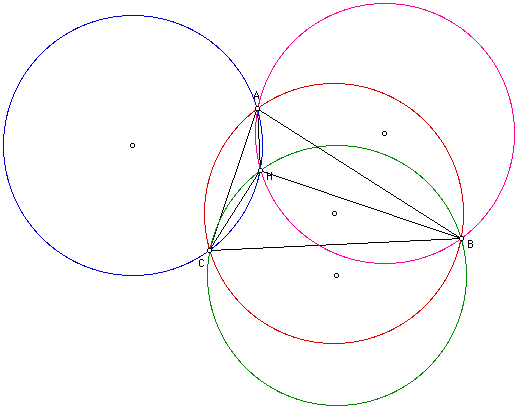
The circumcircles for triangles ABC, ABH, BCH, ACH are red, pink, green, and blue respectively. In order to investigate this construction further click here.
7. Conjectures? Proofs? All four circles are congruent to each other. How do we know this? This is not as easy as we thought. By using GSP, there are many ways to "prove" this, but it is not quite as obvious without the use of GSP. After "hints" from Dr. Wilson and consulting Inchul (who could not explain "why" either), we have taken a break from trying to prove that these circles are congruent. We are simply accepting it on faith. (If anyone reading this assignment knows how to prove it please contact us by email. Thank you.)
9. Construct triangle ABC, its incircle, its three excircles and its nine-point circle. Conjecture?
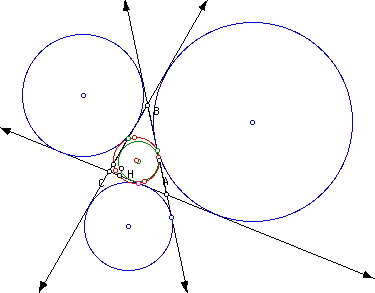
The red circle is the nine-point circle, green is the incircle and the blue are the excircles. To further investigate this construction, click here.
The nine-point circle is always tangent to the incircle and excircles. When the triangle is equilateral, the incircle is also the nine-point circle and the three excircles are congruent to each other. The excircles never touch one another (unless the triangle is degenerate, but then again the circles will no longer be circles.)
Here ends our investigations of altitudes and orthocenters.