

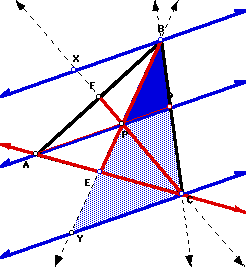
Let's investigate the situation of any triangle ABC with a point P anywhere in the interior of the triangle. I will draw the lines AP, BP, and CP extended to their intersection with the opposite sides of the triangle, respectively points D, E, and F.
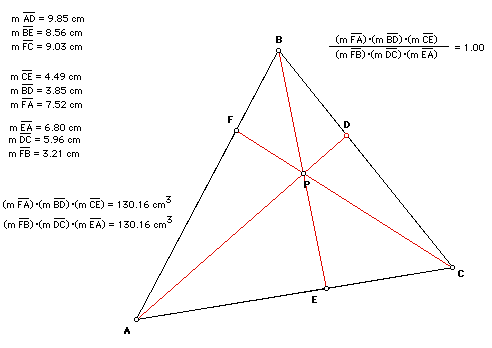
You will see from the picture of the above described situation and measurements that, at least in this particular situation, the ratio
is equal to 1. Clearly, we have several similar triangles shown in the diagram above. Look at the picture when I construct lines BX and CY parallel to segment AD:
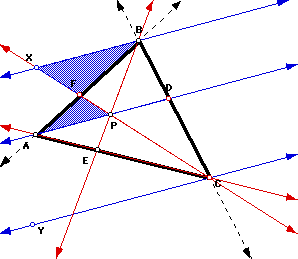
I have shaded two triangles that are formed that happen to be similar, triangle XFB and triangle PFA. In these triangles we find angle AFP congruent to angle BFX since they are vertical to each other. Also, angle XBF is congruent to angle PAF since they are alternate interior angles formed by the parallel lines BX and AD. By the Angle-Angle Similarity Theorem, triangle XFB is similar to triangle PFA. If triangles are similar, then their sides are proportional. Therefore,
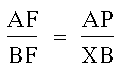 .
.In a similar fashion, look now at triangles AEP and CEY:
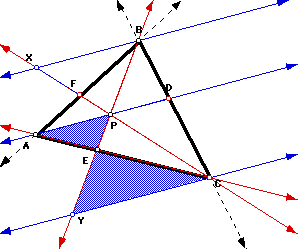
The angles AEP and CEY are vertical to each other and are, therefore, congruent. Also, angle PAE and angle YCE are congruent since they are the alternate interior angles formed by the parallel lines AD and CY. Of course, then, the shaded triangles are similar, once again giving us proportional sides:
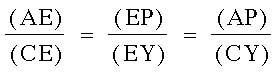 .
.In a similar manner, now let's look at the construction of lines BM and AN that are parallel to CF:
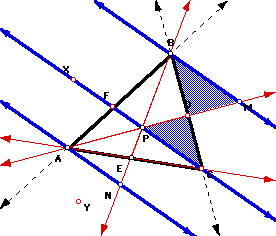
Once again, we can see the triangles BDM and CDP are similar for the same reasons the previous triangles were. This gives us the following ratio of their sides:
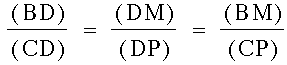 .
.Now, let's look at a couple of different kinds of triangles that are formed, again with the parallel lines that were created to be parallel to line AD, lines BX and CY:
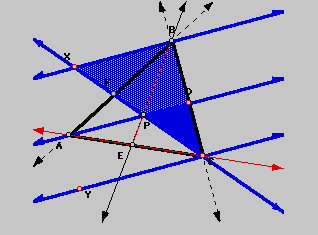
We will be comparing triangles XBC and PDC. First of all, both triangles share the angle at vertex C, namely angles DCP and BCX. Therefore, one pair of angles in the triangles is congruent. Also, angle BXC and angle DPC are congruent since they are corresponding angles formed by the parallel lines. We can safely say, then, that triangle XBC and triangle PDC are similar due to the Angle-Angle Similarity Theorem. This means, also, that the following proportions of their corresponding sides is true as well:
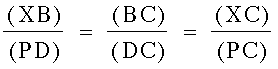
Finally, let's look at one other set of triangles from those formed by our constructed parallel lines:
Triangle BPD and triangle BYC are similar to each other for reasons similar to the situation just above it. The two triangles share an angle and have corresponding angles formed by the parallell lines in them.. We can then look ar their proportional sides:
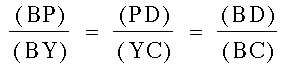 .
.Now we can begin to settle the issue of how our ratio mentioned earlier has a value of 1. I will use the multiplicative property of equality to show how these proportions can be used to manipulate a starting equation:
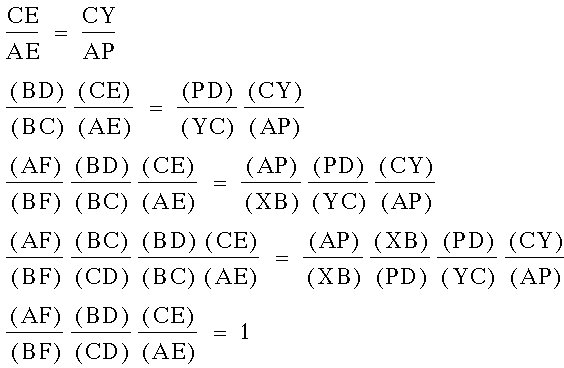
Now we have proof of what our measurements have already shown us.
Let's see what would happen if triangle ABC had been made with lines and P was outside the triangle:
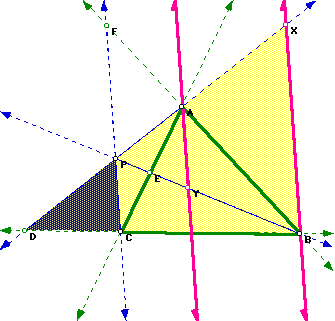
Clearly, we can see the same relationships here as we had in the previous situation with P inside the triangle. We have similar triangles with proportional sides. Click here to investigate more on your own by moving P around.
Look at the areas created by the triangle ABC with point P inside and the parallel lines:
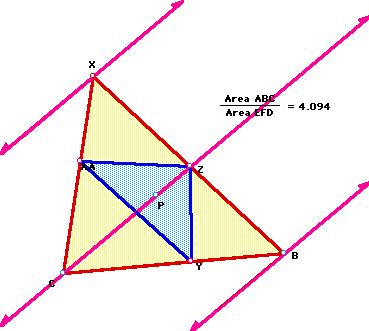
We can see that, at least in this case, the ratio of the areas of triangles ABC to EFD is greater than 4. Look at a couple of other examples where the configuration of the triangle has been changed:
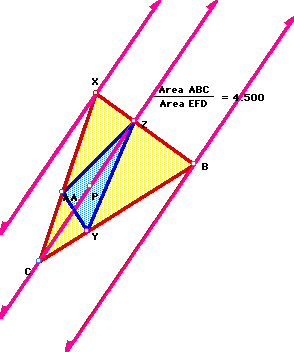
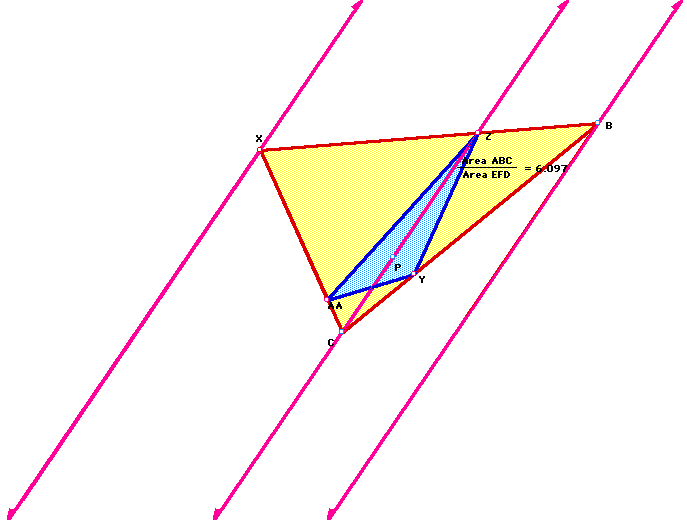
Clearly, in each of the examples, the ratio of the areas of the two triangles is always greater than 4. Click here to see more for yourself. After some investigation of my own, I found that the ratio of the areas is equal to 4 whenever P is at the centroid of the triangle, no matter what kind of triangle we may be using:

Here we see that P is slightly off of the centroid of the triangle, and the ratio of the areas is slightly greater than 4. But look at the situation when I move P to the centroid:
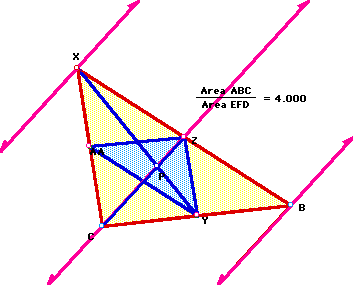
It is clear from my investigation of these areas that the ratio of the areas of triangles ABC to DEF is always greater than or equal to 4. Equality with 4 is dependant upon the placement of P at the centroid of the triangle. Click here to investigate more on your own.