

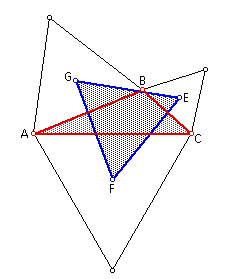
Given any triangle ABC, construct equilateral triangles on each side and find the centroids of each equilateral triangle. Connecting these three centers produces another equilateral triangle called "Napoleon's Triangle".
To learn more about Napoleon Bonaparte click here.
By rotating the original triangle 120 and 240 degrees about the vertices of Napoleon's Triangle:
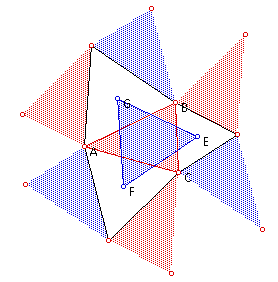
This piece tessellates.

Segments from the original triangle's vertices to the opposite unconnected vertices of the equilateral triangles are concurrent and equal in length. The point of concurrency is called the Fermat point (and is also the point where the circumcircles of the outer equilateral triangles meet).
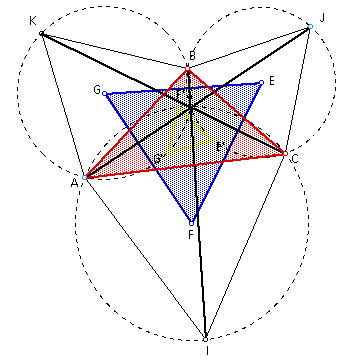
The Fermat point (F) is the point inside a triangle ABC (provided no angle exceeds 120 degrees) such that the sum AJ + BI + CK is a minimum.
By reflecting each endpoint of Napoleon's Triangle across the nearest side of the original triangle produces another equilateral triangle called the inner Napoleon triangle.
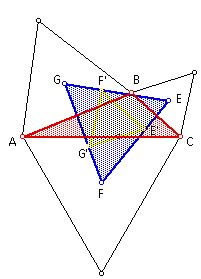
When moving the original triangle, the new triangle disappears when the area of outer Napoleon's triangle is equal to the area of the original triangle. Likewise, when the outer Napoleon's triangle has equal area to the inner Napoleon's triangle, the original triangle converges into a line with no area.
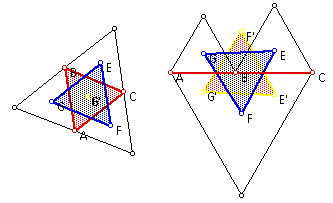
This indicates that the difference of the areas of the two Napoleon triangles is the area of the original triangle. Or, in other words: the sum of the areas of the inner Napoleon triangle and the original triangle is equal the area of the outer Napoleon triangle.