
EMAT 6680

This is an exploration of the parametric equations:
I will explore what happens as the coefficients a,b,c, and d are varied. The range of "t" will be from
0 - 6.28 radians.
First, let's graph x=cos(t) and y=sin(t). Thus, a=b=c=d=1.
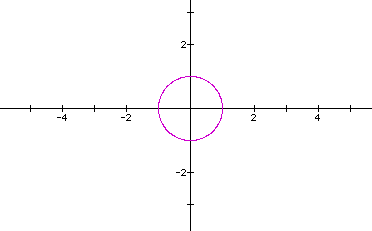
Looks like a circle.
Now, let's look at the curve when a=2,b=1,c=d=1.
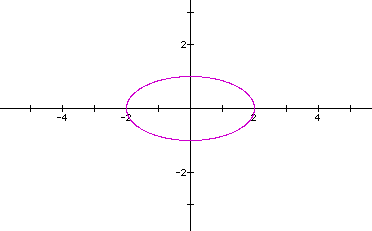
Looks like an ellipse with major axis along the x-axis and minor axis along the y-axis. Notice that when a=2 the curve lies between x=-2 and x=2.
Now, let's look at the curve when a=b=2,c=d=1.
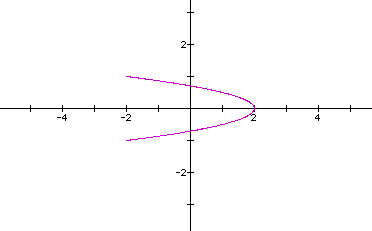
Looks like part of an ellipse or part of a parabola. Why is this?
Let's look at the curve when a=b=c=d=2.
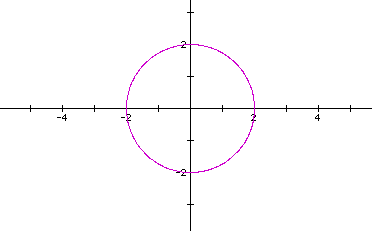
Looks like a circle. This time the radius equals 2.
Let's look at the curve when a=1,b=2,c=d=1.
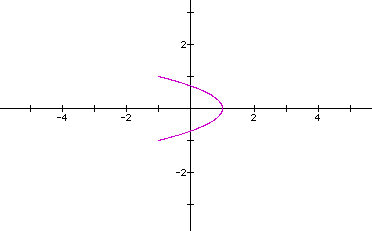
This looks similar to when a=b=2,c=d=1. Notice that the curve lies between x=-1 and x=1; whereas when a=b=2, the curve lies between x=-2 and x=2. Why is this?
Let's continue exploring until we come up with some hypothesis.
Let's look at the curve when a=b=2,c=1,d=2.
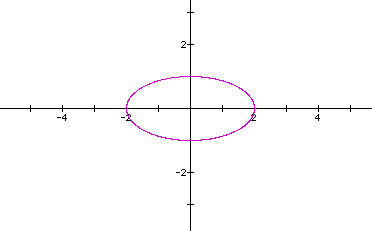
Looks like an ellipse again. This is the same curve as when a=2, b=c=d=1. Any ideas yet?
Let's look at the curve when a=b=2,c=3,d=2.
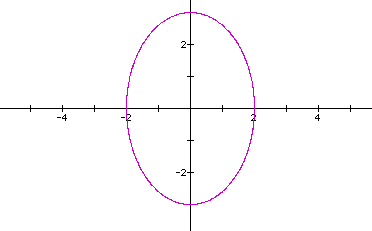
Another ellipse. However, the major axis lies along the y-axis this time. Notice that the curve lies between the interval of y=[-3,3]. Maybe the coefficients a and c determine the length of the curve along the x- and y-axes. But what do the coefficients b and d determine? Let's keep exploring.
Let's look at the curve when a=b=2,c=2,d=1.
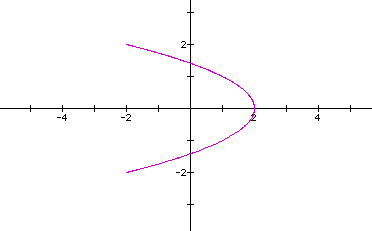
Back to the partial ellipse. The length along the axis is still the same as the values of a and c.
We have looked at a=b=2,c=d=1; a=1,b=2,c=d=1; and a=b=c=2,d=1. So now look at the curve when a=2,b=c=d=1.
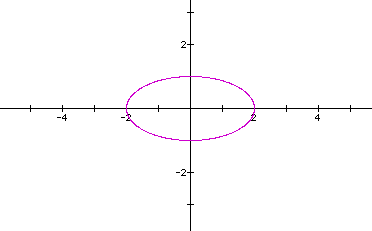
It's an ellipse again. The curve still lies along the intervals associated with [-a,a] for the x-axis and [-c,c] for the y-axis. Still not sure why the partial ellipse shows up yet.
Let's look at the curve when a=b=1,c=2,d=1.
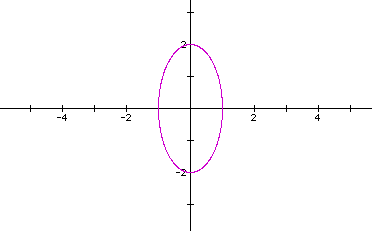
It's an ellipse. Let's look at the curve when a=b=c=1,d=2.
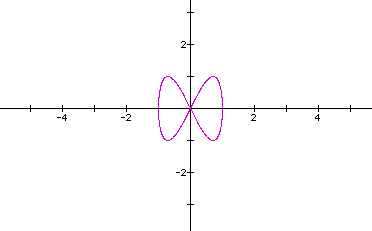
Something different. The curve still lies along the intervals of [-a,a] and [-c,c]. Why is the curve like this?
Let's look at the curve when a=3, b=2, c=3, d=2.
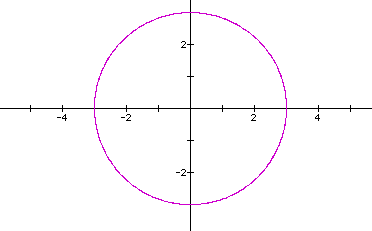
Back to a circle. All the circles have been generated when the ratio of a/c = 1 and the ratio of b/d =1.
So, let's look at the curve when a=3,b=2,c=3,d=1.
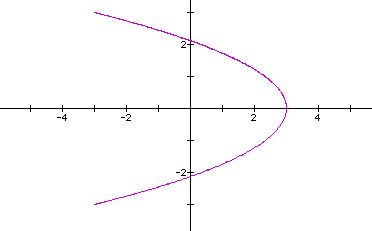
Back to the partial ellipse. Increasing the range of "t" does not change the graph. This was done at an attempt to see if graphing the curve with more than one complete rotation affected the outcome. It did not.
So, let's look at the curve when a=b=2,c=3,d=4.
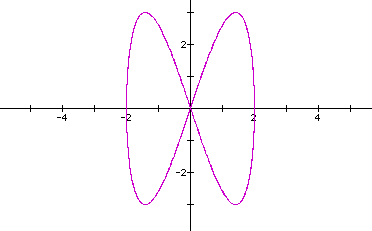
Ok.
How about when a=b=2,c=3,d=6?
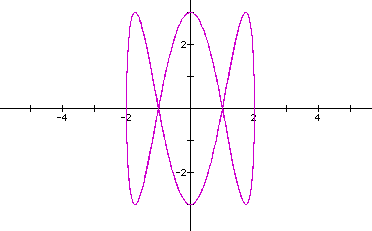
The ratio of b/d is 2/6 or 1/3. So let's look at when a=2,b=1,c=d=3.
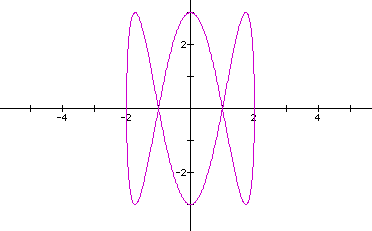
Looks like the same graph. How about when a=b=2,c=2,d=7?
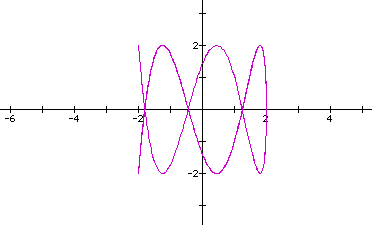
O.K. The ratio of b/d is 1/3.5, and there are3.5 local minumums and maximums at y=+-2.
Let's look at the curve when a=b=2,c=7,d=2.
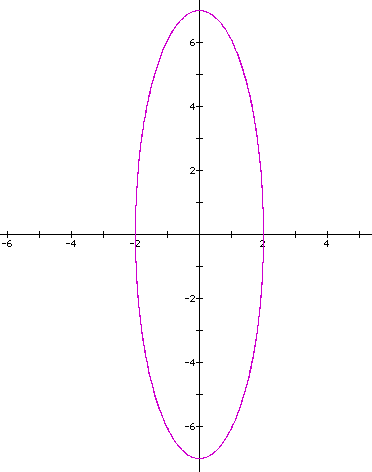
This is an ellipse again. So when the ratio of b/d =1 and the ratio of a/c does not equal 1, then we get an ellipse. If both ratios a/c and b/d equal 1, then we get a circle.
Ok. How does the curve look when a=b=4,c=4,d=7?
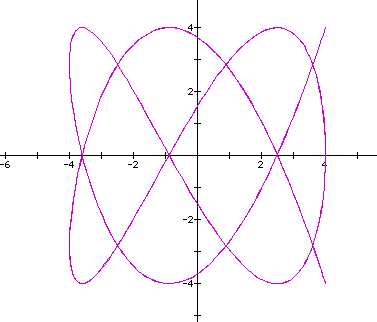
How does the curve look when a=b=4,c=2,d=1?
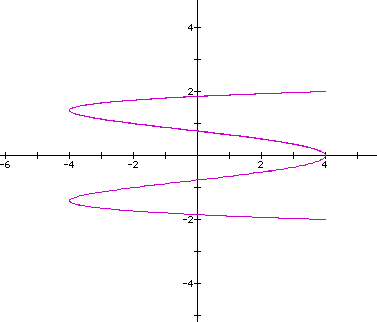
Here the ratio of b/d=4.
Let's look at the curve when a=b=4,c=d=3.
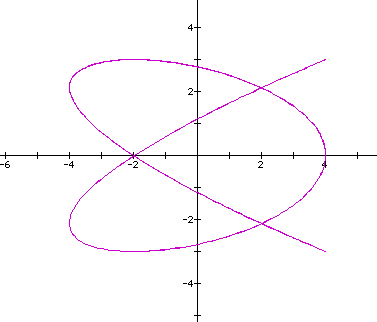
Here the ratio of b/d = 4/3. Let's see what happens when the ratio of b/d=3.5/1 (a=c=3,b=3.5,d=1).
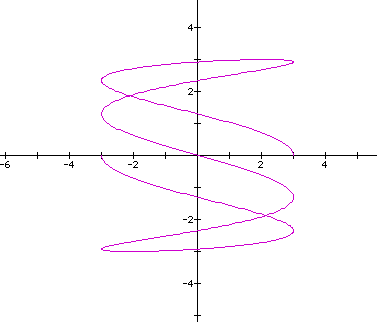
Now, I graphed the curve for t:0 - 12.6 and it looked like this.
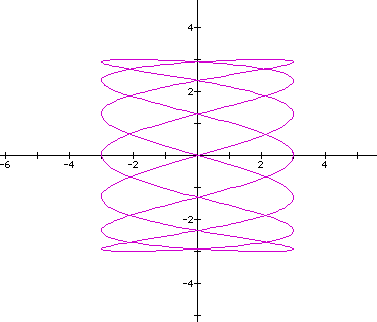
So, the ratio of local min/max for along the horizontal/vertical axes is 14/4=7/2=3.5/1. So let's look at the curve when the ratio of b/d=1/3.5 (a=c=3,b=1,d=3.5) for "t" varying 0 - 6.28.
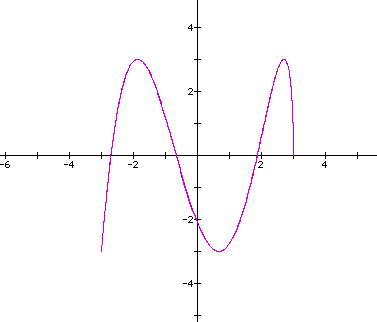
Now when "t" is varied 0 - 12.6.
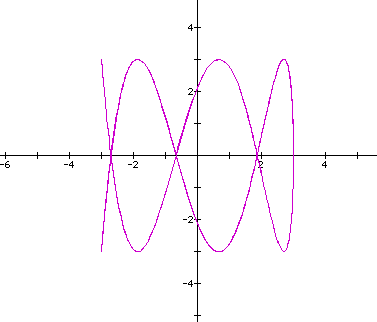
O.K. Let's increase the range of "t" to 0 - 25.2. No change was observed, so the graph is not shown.
Let's look at the curve when a=c=3,b=1,d=4.
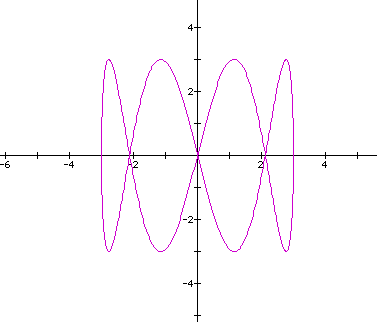
The ratio of b/d=1/4 and the ratio of local min/max along the horizontal/vertical axes is 2/8=1/4. When the ratio of b/d=4/1, the software only graphed half of the curve. I went back, increased the range of "t" from the original 0 - 6.28 to 0 - 25.2 and the result was the same. There must be some software limitation on Graphing Calculator that prevents graphing the entire curve in some cases.
However, a pattern has emerged for this curve as a,b,c, and d are varied. If the ratio of a/c=1 and the ratio of b/d=1, then the curve is a circle. If the ratio of a/c does not equal 1 and the ratio of b/d=1, then the curve is an ellipse. If the ratio of b/d does not equal 1, then the result looks like similar to the sine function reflected about the x-axis. The graph of the curve lies between the intervals [-a,a] along the x-axis and [-c,c] along the y-axis in all cases. The ratio of b/d is the same as the ratio of (the number of local minimums and maximums along the horizontal axis)/(the number of local minimums and maximums along the vetical axis) in all cases.
I do not know if the curve has a special name when the ratio of b/d does not equal 1. I have not asked anyone and have not come across it in any reading. There are still more things to study in this area.
Return to Chris McCord's Home Page