
EMAT 6680

The CENTROID (G) of a triangle is the point of intersection of the three medians. A median is the segment from a vertex of the triangle to the midpoint of the opposite side.
The ORTHOCENTER (H) of a triangle is the common intersection of the three lines containing the altitudes. An altitude is a perpendicular segment from a vertex to the line of the opposite side. (Note: the foot of the perpendicular may be on the extension of the side of the triangle.) It should be clear that H does not have to be on the segments that are the altitudes. Rather, H lies on the lines extended along the altitudes.
The CIRCUMCENTER (C) of a triangle is the point in the
plane equidistant from the three vertices of the triangle. Since
a point equidistant from two points lies on the perpendicular
bisector of the segment determined by the two points, C is on
the perpendicular bisector of each side of the
triangle. Note: C may be outside of the triangle.
Proof that for any triangle H, G, and C are collinear:
Let's start with any triangle ABC:
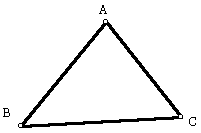
Next, let's construct the orthocenter.
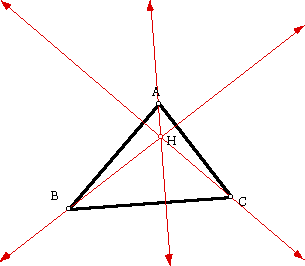
Now, we'll construct the centroid.
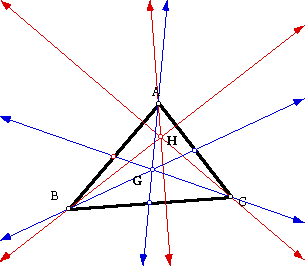
Now we'll construct the circumcenter.
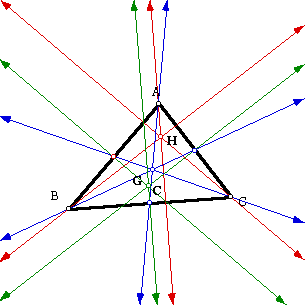
Now, we will hide the red, blue, and green lines and investigate if H, G, and C are collinear.
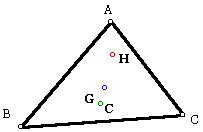
Now, I will construct the line through points G and C. We will then prove that the orthocenter (H) lies on that line.
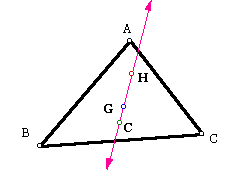
It appears that H lies on the line through G and C. Let's reconstruct the orthocenter and observe that it is indeed on the line GC.
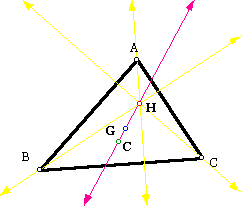
Click here to investigate this triangle and observe that H, G, and C are collinear.
Proof that HG = 2 GC
We will start with triangle ABC and the orthocenter and circumcenter.
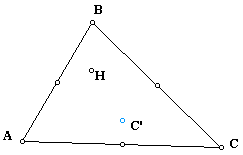
H is the orthocenter and C' is the circumcenter. Thus C'F is the perpendicular bisector of AC. Also, BK is the altitude of triangle ABC.
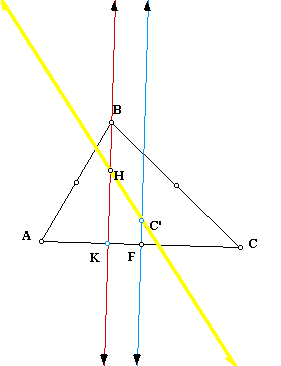
The line through HC is in yellow. Since both C'F and BK are perpendicular to AC, C'F and BK are parallel. So by constructing segment BF and using the alternate interior angle theorem, we see that triangles BHG and FC'G are similar triangles (see below):
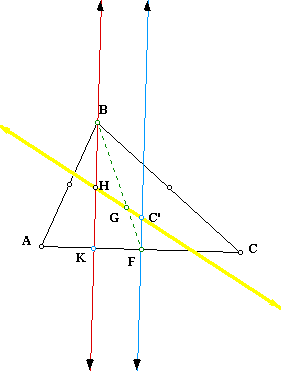
Quick note that if we construct the line through A and the midpoint of BC (which we will label E), then the intersection of this line and the segment BF will define the centroid of triangle ABC. Note that this point is indeed point G and that G is collinear with H and C'. (Thus another way to show that centroid (G), orthocenter (H), and circumcenter (C) are collinear for any triangle.)
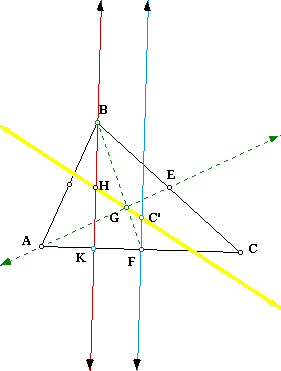
Back to proving that HG = 2 GC.
Since triangles BHG and FC'G are similar, C'G/C'H = BG/GF. But we know that the centroid (G) divides BF such that BG/BF = 2/3 and GF/BF = 1/3. Thus BG = 2 GF.
Or in other words, BG/GF = 2. Thus C'G/C'H = 2.
So C'G = 2 C'H. Which is what is desired.
Therefore for any triangle, HG = 2 GC (where H is the orthocenter, G is the centroid, and C is the circumcenter).
Return to Chris McCord's Home Page