
Write- up # 1

This problem is to explore what happens to the graphs
i. h(x) = f(x) + g(x)
ii. h(x) = f(x) . g(x)
iii. h(x) = f(x)/g(x)
iv. h(x) = f(g(x))
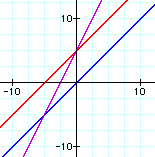
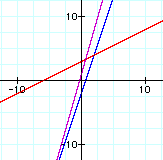
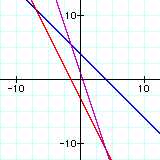
I chose four sets of linear functions to manipulate in each section. I chose a set of parallel lines, a set of intersecting lines with positive slopes, a set of intersecting lines with negative slopes, and a set one with a constant function.
In each set of graphs f(x) and g(x) are colored in red and blue (noted below each graph)
The resulting function formed by the given operations are colored in purple.
i. f(x) + g(x):
 |
 |
 |
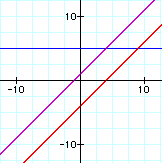 |
In each set of graphs, the sum is always linear.
This is always true, because anytime you add linear terms the sum is linear.
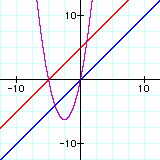
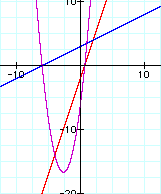
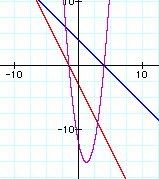
ii. f(x) . g(x)
 |
 |
 |
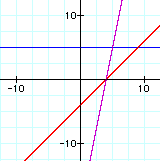 |
In each set of graphs, the graph of the product is a parbola except of the graph with the constant function.
Whenever you are multiplying two linear terms, you will get a quadratic term. Since in the case of the constant function has no linear term, this product remains linear.
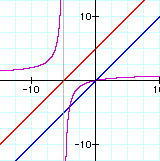
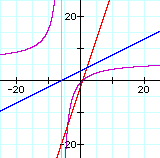
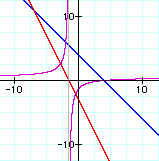
iii. f(x) / g(x):
 |
 |
 |
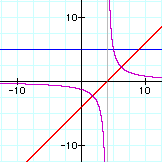 |
In each set of graphs, the graph of the quotient is a hyperbola.
Whenever you divide by a linear term you get 1/x which is a hyperbola.
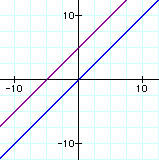
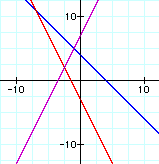
iv. f(g(x))
 |
 |
 |
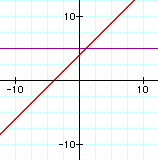 |
In each set of graphs, the graph of the compositions is always linear.
Since in composite functions you replace one linear term with another, the result will be linear.